Cilindro para niños
Un cilindro es una figura geométrica muy común que puedes ver en objetos de tu vida diaria, como una lata de refresco o un rollo de papel. En matemáticas, un cilindro es una forma tridimensional que tiene dos bases paralelas e iguales, y una superficie curva que las conecta.
Imagina una línea recta que se mueve sin cambiar su dirección, siguiendo el borde de una figura plana, como un círculo. Esa línea que se mueve se llama generatriz, y la figura plana que guía su movimiento se llama directriz. El espacio que forma esta línea al moverse es lo que conocemos como cilindro.
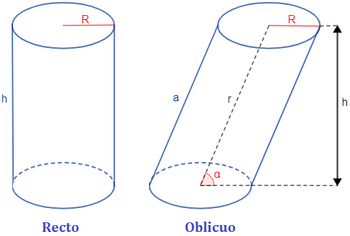
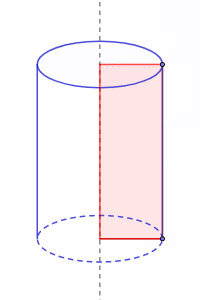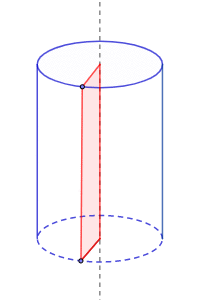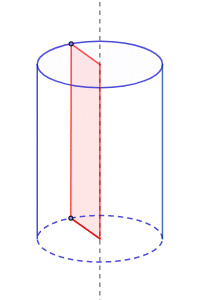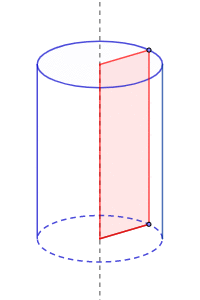
Si la figura plana (directriz) es un círculo y la línea que se mueve (generatriz) es perpendicular a ese círculo, entonces el cilindro que se forma se llama cilindro circular recto. Este tipo de cilindro es como un tubo perfecto, donde todos sus puntos están a la misma distancia de una línea central, llamada el eje del cilindro.
Contenido
Tipos de Cilindros
Los cilindros se pueden clasificar según la posición de su eje respecto a sus bases:
- Cilindro recto: Es cuando el eje del cilindro es perpendicular a sus bases. Piensa en una lata de refresco de pie.
- Cilindro oblicuo: Es cuando el eje del cilindro no es perpendicular a sus bases, sino que está inclinado. Imagina una pila de monedas que se ha deslizado un poco.
Es interesante saber que el volumen de un cilindro recto y el de un cilindro oblicuo pueden ser iguales si tienen la misma base y la misma altura. Sin embargo, el área de su superficie lateral será diferente.
Superficie de un Cilindro
La superficie de un cilindro está formada por las líneas paralelas (generatrices) que conectan las dos bases. Podemos pensar en dos tipos de superficies cilíndricas:
- Superficie cilíndrica de revolución: Se forma cuando todas las líneas generatrices están a la misma distancia de un eje central. Un cilindro circular recto es un ejemplo de esto, ya que se puede formar girando un rectángulo alrededor de uno de sus lados.
- Superficie cilíndrica de no revolución: En este caso, no hay un eje central del que todas las generatrices estén a la misma distancia.
¿Cómo calcular el área de un cilindro?
Para calcular el área total de un cilindro circular recto, necesitamos sumar el área de sus dos bases circulares y el área de su superficie lateral.
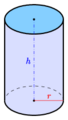
Si el radio de la base es r y la altura del cilindro es h:
- El área de cada base circular es: π multiplicado por el radio al cuadrado (πr²). Como hay dos bases, el área de las bases es:
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A_b = 2\pi r^2
- La superficie lateral del cilindro, si la "desenrollaras", sería un rectángulo. La altura de este rectángulo es la altura del cilindro (h), y su base es la longitud de la circunferencia de la base (2πr). Así, el área lateral es:
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A_l = 2\pi rh
- Por lo tanto, el área total del cilindro es la suma del área de las bases y el área lateral:
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = A_b + A_l : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = 2\pi r^2 + 2\pi rh Esta fórmula también se puede escribir así: : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = 2\pi r (r + h)
Volumen de un Cilindro
El volumen de un cilindro, ya sea recto u oblicuo (siempre que tenga bases circulares), se calcula multiplicando el área de su base por su altura. La altura es la distancia entre las dos bases.
Si el radio de la base es r y la altura es h, el volumen (V) de un cilindro circular es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = \pi r^2h
Esta fórmula es muy útil para saber cuánto líquido puede contener un recipiente con forma de cilindro, como una botella o un tanque.
Galería de imágenes
Véase también
 En inglés: Cylinder Facts for Kids
En inglés: Cylinder Facts for Kids