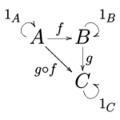Categoría (matemáticas) para niños
En teoría de categorías, una categoría es como un sistema organizado que agrupa "cosas" (llamadas objetos) y "conexiones" o "flechas" (llamadas morfismos) entre esas cosas. Imagina que tienes un montón de puntos y flechas que los unen. Una categoría establece reglas sobre cómo estas flechas pueden combinarse y qué propiedades deben tener.
Por ejemplo, una categoría muy común es la de los conjuntos. Aquí, los objetos son todos los conjuntos que existen, y las flechas son las funciones que van de un conjunto a otro. La forma de combinar flechas es la misma que la de combinar funciones.
En general, los objetos y las flechas pueden ser cualquier tipo de elementos abstractos. La idea principal de las categorías es ofrecer una forma fundamental y abstracta de describir diferentes conceptos matemáticos y cómo se relacionan entre sí. Es una rama de las matemáticas que busca unir y generalizar muchas otras áreas, revelando conexiones profundas entre temas que parecen muy distintos.
Dos categorías se consideran iguales si tienen los mismos objetos, las mismas flechas y las mismas reglas para combinar esas flechas. A menudo, las categorías se nombran con abreviaciones de los objetos que contienen, como Con para la categoría de conjuntos, Top para la categoría de espacios topológicos o Ab para la categoría de grupos abelianos.
Contenido
¿Qué es una Categoría en Matemáticas?
Una categoría es una estructura matemática que nos ayuda a entender cómo se relacionan diferentes tipos de "cosas" matemáticas. Piensa en ella como un mapa donde los lugares son los "objetos" y los caminos son las "flechas" o "morfismos".
¿Cómo se define una Categoría?
Una categoría C tiene:
- Una colección de objetos, que se escribe ob(C).
- Para cada par de objetos A y B en ob(C), hay un grupo de flechas o morfismos que van de A a B. Esto se escribe C(A,B).
- Una forma de componer flechas: si tienes una flecha f de A a B y otra flecha g de B a C, puedes combinarlas para obtener una nueva flecha g ∘ f que va directamente de A a C.
Además, se deben cumplir dos reglas importantes:
- Asociatividad: Si tienes tres flechas f, g, h que se pueden componer en orden, no importa cómo las agrupes al componerlas. Es decir, h ∘ (g ∘ f) es lo mismo que (h ∘ g) ∘ f.
- Identidad: Para cada objeto A, existe una flecha especial llamada flecha de identidad (escrita 1A) que va de A a sí mismo. Esta flecha actúa como un "elemento neutro" al componerse: si combinas cualquier flecha f con la identidad, el resultado es la misma flecha f.
¿Quiénes inventaron las Categorías?
La idea de categoría y los primeros conceptos de la teoría de categorías fueron presentados por primera vez en 1945. Los matemáticos Samuel Eilenberg y Saunders Mac Lane los introdujeron en un artículo llamado "Teoría general de las equivalencias naturales".
Ejemplos de Categorías
Las categorías se usan para describir muchas áreas de las matemáticas. Aquí tienes algunos ejemplos:
La Categoría de Conjuntos
La categoría Con es una de las más usadas. Sus objetos son todos los conjuntos, y sus flechas son las funciones que van de un conjunto a otro. La composición de flechas es simplemente la composición normal de funciones.
Categorías con un solo objeto
- Un monoide es una estructura matemática con una operación que se puede combinar de forma asociativa y tiene un elemento neutro. Puedes pensar en un monoide como una categoría que tiene un solo objeto. Las flechas de este objeto a sí mismo son los elementos del monoide, y la composición de flechas es la operación del monoide.
- Un grupo es un tipo especial de monoide donde cada elemento tiene un "inverso". Un grupo también puede verse como una categoría con un solo objeto, donde todas las flechas tienen una flecha inversa.
Categorías de gráficos
Cualquier gráfico dirigido (un conjunto de puntos conectados por flechas) puede formar una categoría pequeña. Los objetos son los puntos del gráfico, y las flechas son los caminos que puedes seguir a lo largo del gráfico. La composición de flechas es simplemente unir los caminos.
Tipos de Flechas (Morfismos)
Las flechas en una categoría pueden tener propiedades especiales:
- Un monomorfismo es una flecha que, si la combinas con otras dos flechas y el resultado es el mismo, entonces esas dos flechas originales deben ser iguales. Piensa en ella como una flecha "inyectiva".
- Un epimorfismo es una flecha que, si la combinas con otras dos flechas y el resultado es el mismo, entonces esas dos flechas originales deben ser iguales. Piensa en ella como una flecha "sobreyectiva".
- Un isomorfismo es una flecha que tiene una flecha "inversa". Si una flecha es un isomorfismo, significa que los dos objetos que conecta son "esencialmente los mismos" desde el punto de vista de la categoría.
Tipos de Categorías
Existen diferentes tipos de categorías, cada una con propiedades adicionales:
- Una categoría aditiva es un tipo de categoría donde las flechas entre dos objetos no son solo un conjunto, sino que tienen una estructura de grupo que es compatible con la composición.
- Una categoría abeliana es un tipo especial de categoría aditiva que tiene propiedades adicionales que la hacen muy útil para estudiar estructuras algebraicas como los grupos abelianos. La categoría de grupos abelianos (Ab) es un ejemplo clásico.
- Una categoría completa es aquella donde ciertos tipos de "límites" matemáticos siempre existen. Las categorías de conjuntos y espacios topológicos son ejemplos de categorías completas.
Galería de imágenes
-
Esta es una categoría con una colección de objetos A, B, C y colección de morfismos denominados f, g, g ∘ f, y los lazos son las flechas identidad. Esta categoría por lo general se identifica por el 3 en negrita.
-
Un gráfico dirigido.
Véase también
En inglés: Category (mathematics) Facts for Kids
