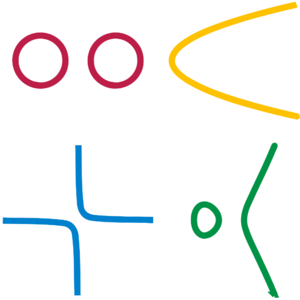Variedad (matemáticas) para niños
Una variedad es un concepto matemático que nos ayuda a entender formas y espacios que pueden ser curvos, pero que si los miramos de cerca, parecen planos. Imagina la superficie de la Tierra: es redonda, pero si estás en un campo, parece plana. Una variedad es como una superficie o una curva, pero puede tener cualquier número de dimensiones.
Por ejemplo, una línea es una variedad de una dimensión. Una superficie, como la de una pelota, es una variedad de dos dimensiones. Las variedades nos permiten estudiar estas formas complejas usando herramientas de la geometría plana.
Plantilla:Ficha de concepto matemático
Contenido
¿Qué es una variedad?
Una variedad es un espacio que, aunque globalmente puede ser curvo o complicado, si lo observamos en una pequeña parte, se parece mucho a un espacio plano.
Los mapas o cartas
Piensa en cómo usamos mapas para orientarnos en la Tierra. La Tierra es una esfera, pero los mapas son planos. Para cubrir toda la Tierra, necesitamos muchos mapas. Cada mapa muestra una parte de la Tierra. En los bordes de los mapas, hay información para "unirlos" mentalmente con los mapas vecinos.
En matemáticas, usamos algo similar llamado "cartas" o "mapas" para describir una variedad. Una carta es como una porción de la variedad que podemos "aplanar" para estudiarla. Un "atlas" es la colección de todas estas cartas que cubren la variedad completa.
Por ejemplo, para describir un círculo, podemos usar dos arcos que se superponen. Cada arco es una "carta" que nos permite ver una parte del círculo como si fuera una línea recta.
Generalmente, no podemos describir una variedad con una sola carta. Esto se debe a que la forma global de la variedad es diferente de la forma simple de un espacio plano. Por ejemplo, ningún mapa plano puede representar toda la Tierra sin distorsiones.
Dimensiones de las variedades
La dimensión de una variedad nos dice cuántos números necesitamos para ubicar un punto en ella.
- Las curvas son variedades de una dimensión. Solo necesitas un número (como la distancia a lo largo de la curva) para saber dónde estás.
- Las superficies son variedades de dos dimensiones. Necesitas dos números (como la latitud y la longitud en la Tierra) para encontrar un punto.
- Existen variedades de más de dos dimensiones. Aunque son difíciles de dibujar, los matemáticos las estudian usando herramientas especiales.
Todas las variedades de la misma dimensión se parecen localmente. Por ejemplo, una pequeña parte de cualquier curva se parece a una línea recta. Una pequeña parte de cualquier superficie se parece a un plano. Sin embargo, las variedades se distinguen por su forma global. Por ejemplo, un círculo y una parábola son curvas, pero no puedes transformar una en la otra sin romperla.
Tipos de variedades
Existen diferentes tipos de variedades, cada una con propiedades especiales:
Variedades topológicas
Las variedades topológicas son las más básicas. Se parecen a un espacio plano normal en cada punto. Imagina que puedes estirar o doblar una variedad topológica sin romperla ni pegarla.
Variedades diferenciables
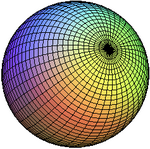
Las variedades diferenciables son un tipo especial de variedades topológicas que son "suaves", sin esquinas ni picos. Esto significa que podemos usar herramientas del cálculo (como derivadas) en ellas. La superficie de una esfera es un buen ejemplo de variedad diferenciable.
Variedades riemannianas
Las variedades riemannianas son variedades diferenciables que tienen una forma de medir distancias y ángulos. Esto nos permite calcular la longitud de las curvas, el área de las superficies y el volumen de los espacios en estas variedades. Son muy importantes en física, por ejemplo, para describir el espacio-tiempo.
Grupos de Lie
Un grupo de Lie es un tipo de variedad que también tiene una estructura de grupo, lo que significa que puedes "sumar" o "multiplicar" sus elementos de una manera suave y continua. Un ejemplo es el grupo de todas las rotaciones en un plano.
Ejemplo: El círculo
El círculo es un ejemplo sencillo de variedad. Podemos pensarlo como un círculo dibujado en un plano. Su ecuación es x² + y² = 1.
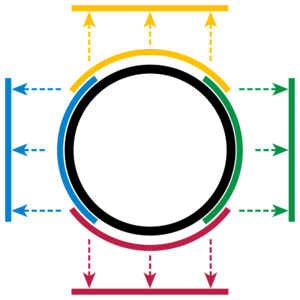
Localmente, el círculo parece una línea recta. Solo necesitamos una coordenada para describir un pequeño arco. Por ejemplo, la parte superior del círculo (la parte amarilla en la Figura 1) se puede describir solo con la coordenada 'x'. Esta es una "carta".
De manera similar, podemos tener cartas para la parte inferior (roja), izquierda (azul) y derecha (verde) del círculo. Juntas, estas cuatro cartas cubren todo el círculo y forman un "atlas".
Cuando dos cartas se superponen, podemos crear una "función de transición" que nos permite pasar de las coordenadas de una carta a las coordenadas de la otra. Esto asegura que las cartas "encajen" bien.
Construcción de variedades
Podemos construir variedades de varias maneras:
Producto de variedades
Si tenemos dos variedades, podemos "multiplicarlas" para crear una nueva variedad de mayor dimensión. La dimensión de la nueva variedad será la suma de las dimensiones de las variedades originales. Por ejemplo, un cilindro se puede construir multiplicando un círculo (1D) por un segmento de línea (1D), resultando en una superficie (2D).

Pegado de variedades
Podemos "pegar" dos variedades de la misma dimensión. Para hacer esto, cortamos un pequeño "agujero" en cada variedad y luego unimos los bordes de esos agujeros. Esto nos permite crear formas más complejas.
Cociente de variedades
Esta forma de construir variedades implica "identificar" o "pegar" puntos de una variedad que se relacionan de cierta manera. Esto puede crear nuevas formas y, a veces, reducir la dimensión.
Propiedades de las variedades
Como las variedades de dimensiones altas son difíciles de visualizar, los matemáticos usan "invariantes" para describirlas. Los invariantes son propiedades que no cambian, sin importar cómo se represente la variedad. Nos ayudan a distinguir una variedad de otra.
Orientabilidad

Una propiedad importante es la "orientabilidad". Imagina que puedes moverte por la superficie de una variedad. Si siempre puedes distinguir tu "izquierda" de tu "derecha" de manera consistente, la variedad es orientable. Ejemplos de variedades orientables son una esfera o un cilindro.
Si no puedes hacerlo, la variedad es "no orientable". El ejemplo más famoso es la cinta de Möbius. Es una superficie con una sola cara y un solo borde. Si dibujas una línea en el centro de la cinta, puedes recorrerla y volver al punto de partida, pero en el lado "opuesto" de donde empezaste. Esto significa que no tiene un "interior" y un "exterior" claros. La Botella de Klein es otro ejemplo de superficie no orientable.
Género y característica de Euler
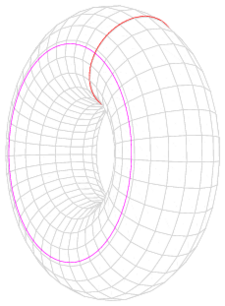
Para las variedades de dos dimensiones, el género es una propiedad clave. El género es el número de "agujeros" o "asas" que tiene una superficie. Por ejemplo, una esfera tiene género 0 (sin agujeros), y un toro (forma de dona) tiene género 1 (un agujero).
En variedades de dimensiones más altas, el género se reemplaza por la característica de Euler, que es un número que también describe la forma global de la variedad.
Aplicaciones de las variedades
Las variedades se usan en muchas áreas de las matemáticas y la física.
En matemáticas
Las variedades son fundamentales en el estudio de formas y espacios complejos. Se utilizan para entender grupos de transformaciones (como las rotaciones) y para extender conceptos del cálculo a espacios más generales.
En física
Las variedades son esenciales en la física moderna. Por ejemplo, se usan para describir el espacio-tiempo en la Teoría de la Relatividad de Einstein. También se aplican en la mecánica clásica para describir el "espacio de configuración" de sistemas, como la posición de un péndulo doble.
Galería de imágenes
-
Bernhard Riemann fue el primer matemático que definió el concepto de variedad.
Véase también
 En inglés: Manifold Facts for Kids
En inglés: Manifold Facts for Kids