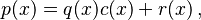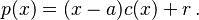Teorema del resto para niños

El teorema del resto es una regla muy útil en el álgebra. Nos dice que cuando divides un polinomio (una expresión con números y letras elevadas a potencias, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 3x - 5 ) entre una expresión sencilla como , el resto que obtienes es igual a lo que resultaría si sustituyeras la letra por el número en el polinomio original.

Esto se entiende mejor si recordamos cómo funciona la división normal. Cuando divides un número, por ejemplo, 10 entre 3, obtienes un cociente (3) y un resto (1). La fórmula es:

Dividendo = Divisor × Cociente + Resto

En el caso de los polinomios, funciona igual:

Aquí, 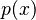es el polinomio que estamos dividiendo (el dividendo), Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q(x) es el polinomio por el que dividimos (el divisor), Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c(x) es el resultado de la división (el cociente) y 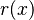es lo que sobra (el resto). Una regla importante es que el grado del resto siempre es menor que el grado del divisor.

Si nuestro divisor es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q(x) = x-a , que tiene un grado de 1, entonces el resto 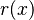debe tener un grado menor que 1. Esto significa que 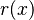es solo un número, una constante, a la que podemos llamar . Así, la fórmula de la división se convierte en:

Ahora, si sustituimos la por el valor en esta ecuación, obtenemos:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{}{}p(a)=(a-a)c(a) + r

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{}{}p(a)=(0)c(a) + r

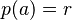
¡Y ahí lo tienes! El resto es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(a) .

El teorema del resto es muy útil porque nos permite encontrar el valor de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(a) sin tener que hacer toda la división del polinomio. También nos ayuda a entender el teorema del factor, que es muy importante para simplificar polinomios.

¿Cómo aplicar el Teorema del Resto?

Para entender mejor cómo funciona este teorema, veamos un ejemplo práctico.

Un ejemplo práctico

Imagina que tenemos el polinomio 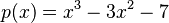. Queremos dividir este polinomio entre .

Si hacemos la división, obtenemos que el cociente es 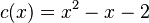y el resto es .

Según el teorema del resto, si sustituimos por 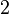en nuestro polinomio original 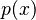, el resultado debería ser el resto, que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -11 . Vamos a comprobarlo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(2) = (2)^3 - 3(2)^2 - 7 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(2) = 8 - 3(4) - 7 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(2) = 8 - 12 - 7 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(2) = -4 - 7 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(2) = -11

¡Funciona! Podemos asegurar que sin necesidad de hacer la división completa.

El Teorema del Factor: ¿Qué es y para qué sirve?

El teorema del factor es una consecuencia directa del teorema del resto. Nos dice que una expresión como es un "factor" de un polinomio (es decir, el polinomio se puede dividir exactamente por sin dejar resto) si y solo si .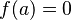

En otras palabras, si al sustituir por en el polinomio el resultado es cero, significa que es uno de los "bloques de construcción" del polinomio, y el resto de la división es cero. Esto es muy útil para encontrar las raíces de un polinomio o para simplificarlo.

Véase también

En inglés: Polynomial remainder theorem Facts for Kids