Teorema de la raíz racional para Niños

El teorema de la raíz racional, también conocido como el teorema de Gauss, es una herramienta muy útil en el álgebra. Nos ayuda a encontrar las posibles soluciones que son números racionales (es decir, fracciones) para ciertas ecuaciones polinómicas.

Imagina que tienes una ecuación como esta:

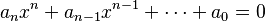
$a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0 = 0\,\!$

Aquí, las letras con números pequeños (como 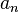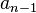$a_n$ , $a_{n-1}$ , etc.) son números enteros (números sin decimales, como 1, -2, 5, 0). El teorema de la raíz racional nos dice que si esta ecuación tiene una solución que es una fracción (llamada raíz racional), esa fracción debe seguir unas reglas muy específicas.

Contenido

¿Qué Dice el Teorema de la Raíz Racional?
- ¿Por Qué es Útil este Teorema?
Cómo Usar el Teorema: Un Ejemplo Práctico
Véase también

¿Qué Dice el Teorema de la Raíz Racional?

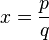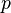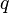Si una ecuación polinómica con coeficientes enteros tiene una solución que es una fracción $x=\frac{p}{q}$ (donde $p$ y $q$ son números enteros y no tienen factores comunes, es decir, son coprimos), entonces:

El número de arriba de la fracción ( 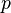$p$ ) debe ser un divisor del último número de la ecuación ( 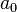$a_0$ , el término independiente).
El número de abajo de la fracción ( 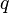$q$ ) debe ser un divisor del primer número de la ecuación ( 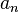$a_n$ , el coeficiente principal).

Este teorema es como un filtro que nos ayuda a reducir la cantidad de posibles soluciones racionales que tenemos que probar.

¿Por Qué es Útil este Teorema?

El teorema de la raíz racional es muy útil porque nos da una lista limitada de posibles soluciones racionales. En lugar de probar infinitas fracciones, solo necesitamos revisar un grupo pequeño de ellas. Si ninguna de las fracciones de esa lista funciona, entonces sabemos que la ecuación no tiene soluciones racionales.

El teorema de la raíz entera es un caso especial de este teorema. Ocurre cuando el coeficiente principal (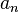 $a_n$ ) es 1. En ese caso, las únicas posibles raíces racionales son números enteros que son divisores del término independiente ( $a_0$ ).

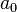Cómo Usar el Teorema: Un Ejemplo Práctico

Vamos a usar el teorema con un ejemplo para entenderlo mejor. Considera la siguiente ecuación:

$3x^3 - 5x^2 + 5x - 2 = 0\,\!$

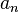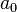Aquí, el coeficiente principal ( $a_n$ , el número que acompaña a la $x$ con el exponente más alto) es 3. El término independiente ( $a_0$ , el número que no tiene $x$ ) es -2.

Para encontrar las posibles soluciones racionales 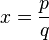$x=\frac{p}{q}$ , seguimos las reglas:

p debe ser un divisor de 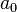$a_0$ (que es -2). Los divisores de -2 son: ±1, ±2.
q debe ser un divisor de 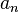$a_n$ (que es 3). Los divisores de 3 son: ±1, ±3.

Ahora, formamos todas las posibles fracciones $\frac{p}{q}$ con estos divisores:

Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q=1 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{1}=1 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-1}{1}=-1 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{2}{1}=2 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-2}{1}=-2 .
Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): q=3 : $\frac{1}{3}$ , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-1}{3} , $\frac{2}{3}$ , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{-2}{3} .

Así, la lista de posibles soluciones racionales para esta ecuación es: 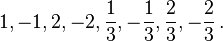$1, -1, 2, -2, \frac{1}{3}, -\frac{1}{3}, \frac{2}{3}, -\frac{2}{3}\,.$

Ahora, podemos probar cada uno de estos números en la ecuación para ver cuál la hace verdadera. Por ejemplo, si probamos $x = 1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3(1)^3 - 5(1)^2 + 5(1) - 2 = 3 - 5 + 5 - 2 = 1 Como el resultado es 1 y no 0, $x=1$ no es una solución.

Si probamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = \frac{2}{3} : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3\left(\frac{2}{3}\right)^3 - 5\left(\frac{2}{3}\right)^2 + 5\left(\frac{2}{3}\right) - 2 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): = 3\left(\frac{8}{27}\right) - 5\left(\frac{4}{9}\right) + \frac{10}{3} - 2 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): = \frac{8}{9} - \frac{20}{9} + \frac{30}{9} - \frac{18}{9} Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): = \frac{8 - 20 + 30 - 18}{9} = \frac{0}{9} = 0 ¡Encontramos una solución! Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = \frac{2}{3} es una raíz racional de la ecuación.

Este proceso nos ayuda a encontrar las soluciones racionales de manera más eficiente.

Véase también

En inglés: Rational root theorem Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Teorema_de_la_raíz_racional&oldid=5004269»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Teorema de la raíz racional para Niños. Enciclopedia Kiddle.

Teorema de la raíz racional para niños

Contenido

¿Qué Dice el Teorema de la Raíz Racional?

¿Por Qué es Útil este Teorema?

Cómo Usar el Teorema: Un Ejemplo Práctico

Véase también