Resistencia (fluidos) para niños
En el mundo de la física, cuando un objeto se mueve a través de un líquido o un gas (a los que llamamos fluidos), experimenta una fuerza que se opone a su movimiento. Esta fuerza se llama resistencia o fricción de fluido. Piensa en cuando nadas en el agua o cuando el viento empuja tu bicicleta: esa es la resistencia en acción.
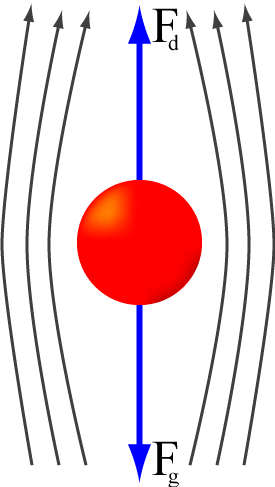
Si el fluido es agua, la resistencia se llama resistencia hidrodinámica. Si es aire, se llama resistencia aerodinámica. Esta fuerza siempre actúa en dirección opuesta al movimiento del objeto. Por ejemplo, en un coche o un avión, la resistencia aerodinámica es lo que el motor debe vencer para que el vehículo avance.
Aunque a veces no la notamos, la resistencia es muy importante. Por ejemplo, es clave para entender cómo se mueven las pelotas en los deportes, cómo vuelan los aviones o cómo los corredores y nadadores logran sus récords. Incluso en la Fórmula 1, los coches necesitan una gran resistencia aerodinámica para pegarse al suelo y no salir volando.
Contenido
Ejemplos de Resistencia en la Vida Diaria
La resistencia de los fluidos se ve en muchos lugares. Por ejemplo, cuando un coche, un avión o un barco se mueven, el aire o el agua los frenan. También es lo que permite que las velas de un barco de vela capturen el viento y lo impulsen.
En los deportes, la resistencia es fundamental. Ayuda a explicar cómo se mueven las pelotas de fútbol o baloncesto, cómo una jabalina vuela por el aire, o cómo un nadador avanza en el agua. La forma de los objetos y la velocidad a la que se mueven influyen mucho en cuánta resistencia experimentan.
Tipos de Resistencia: ¿Qué la Causa?
La resistencia se puede dividir en diferentes tipos, según lo que la cause:
- Resistencia por forma: Esta resistencia depende del tamaño y la forma del objeto. Un objeto con una forma más "redonda" o "aerodinámica" tendrá menos resistencia que uno con una forma "cuadrada" o "plana" que se oponga más al flujo del fluido.
- Resistencia por fricción de superficie: Esta se debe al roce entre el fluido y la superficie del objeto. Imagina que la superficie del objeto es rugosa; el fluido se "pegará" un poco más y creará más fricción. Si la superficie es lisa, habrá menos fricción.
Un objeto se considera "romo" si la mayor parte de su resistencia viene de su forma (como un camión), y "aerodinámico" si la resistencia por fricción es más importante (como un ala de avión). Los coches suelen ser cuerpos romos, mientras que los aviones buscan ser muy aerodinámicos para reducir la resistencia.
Otros tipos de resistencia incluyen:
- Resistencia inducida: Aparece cuando las alas de un avión generan sustentación (la fuerza que lo mantiene en el aire).
- Resistencia ondulatoria: Se produce a velocidades muy altas, cercanas o superiores a la velocidad del sonido, cuando el objeto crea ondas de choque en el fluido.
- Resistencia por formación de olas: Ocurre cuando un barco se mueve por el agua y genera olas.
¿Cómo se Calcula la Resistencia?
La fuerza de resistencia depende de varias cosas: qué tan denso es el fluido, qué tan rápido se mueve el objeto, el tamaño del objeto y su forma. Hay una fórmula para calcularla:
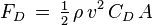
Donde:
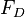 es la fuerza de resistencia (cuánto frena al objeto).
es la fuerza de resistencia (cuánto frena al objeto).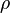 es la densidad del fluido (qué tan "pesado" es el aire o el agua).
es la densidad del fluido (qué tan "pesado" es el aire o el agua).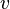 es la velocidad del objeto.
es la velocidad del objeto. es el área frontal del objeto (cuánto "corta" el fluido).
es el área frontal del objeto (cuánto "corta" el fluido).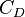 es el coeficiente de resistencia, un número que nos dice qué tan aerodinámico es el objeto. Una forma más aerodinámica tiene un
es el coeficiente de resistencia, un número que nos dice qué tan aerodinámico es el objeto. Una forma más aerodinámica tiene un 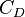 más bajo.
más bajo.
Esta fórmula nos dice que si duplicas la velocidad de un objeto, la fuerza de resistencia se cuadruplica. Esto significa que se necesita mucha más energía para ir más rápido. Por ejemplo, un coche que va al doble de velocidad necesita ocho veces más potencia para vencer la resistencia del aire.
Velocidad Terminal: El Límite de Caída
Cuando un objeto cae, la gravedad lo acelera. Pero a medida que gana velocidad, la resistencia del aire (o del fluido) también aumenta. Llega un punto en que la fuerza de resistencia es igual a la fuerza de la gravedad. En ese momento, el objeto deja de acelerar y cae a una velocidad constante, que se llama velocidad terminal.
Por ejemplo, una gota de lluvia cae a su velocidad terminal. Un paracaidista también la alcanza antes de abrir el paracaídas. Los objetos más grandes y densos tienen una velocidad terminal más alta que los pequeños y ligeros. Por eso, un ratón puede caer desde una gran altura y sobrevivir, mientras que un humano no.
Resistencia a Bajas Velocidades: La Ley de Stokes
Cuando los objetos son muy pequeños o se mueven muy lento en un fluido, la resistencia se comporta de manera diferente. En estos casos, la fuerza de resistencia es directamente proporcional a la velocidad. Esto se conoce como la Ley de Stokes. Es importante para entender cómo se mueven partículas muy pequeñas, como el polen en el aire o las bacterias en el agua.
Aerodinámica: El Arte de Reducir la Resistencia
La aerodinámica es la ciencia que estudia cómo el aire interactúa con los objetos en movimiento. Su objetivo principal es reducir la resistencia para que los vehículos (aviones, coches, trenes) sean más eficientes y rápidos.
Los ingenieros y diseñadores trabajan mucho para dar a los objetos formas que "corten" el aire de la mejor manera posible, minimizando la resistencia. Esto se logra suavizando las superficies, eliminando partes que sobresalgan y diseñando formas que permitan que el aire fluya sin crear turbulencias.
Resistencia Inducida y Resistencia Parásita
En la aviación, la resistencia se divide en dos tipos principales:
- Resistencia inducida: Es la resistencia que se crea por el hecho de que el ala produce sustentación. A bajas velocidades, cuando el avión necesita un ángulo de ataque alto para mantenerse en el aire, esta resistencia es mayor.
- Resistencia parásita: Es la resistencia causada por el movimiento del avión a través del aire, sin contar la sustentación. Incluye la resistencia por la forma del avión y la fricción del aire con su superficie. A medida que la velocidad aumenta, esta resistencia también lo hace.
La combinación de estas dos resistencias crea una curva de resistencia total. Los pilotos buscan volar a la velocidad donde esta resistencia total es mínima, lo que les permite ahorrar combustible y volar de manera más eficiente.
Galería de imágenes
Véase también
 En inglés: Drag (physics) Facts for Kids
En inglés: Drag (physics) Facts for Kids





