Racionalización de radicales para niños
En Matemática, la racionalización de radicales es un proceso importante que nos ayuda a simplificar expresiones. Imagina que tienes una fracción donde el número de abajo (el denominador) tiene una raíz (como una raíz cuadrada o cúbica). La racionalización consiste en transformar esa fracción en otra que sea igual, pero que ya no tenga una raíz en el denominador.
Esto se hace multiplicando la parte de arriba (el numerador) y la parte de abajo (el denominador) de la fracción por una expresión especial. El objetivo es que, al hacer la multiplicación, la raíz del denominador desaparezca. A veces, la raíz puede aparecer en el numerador, ¡y eso está bien!
¿Por qué es útil la racionalización?
La racionalización se usaba mucho antes, cuando no teníamos calculadoras ni ordenadores. Al quitar las raíces del denominador, era más fácil hacer cálculos a mano y obtener resultados más precisos.
Hoy en día, las calculadoras y los ordenadores hacen estos cálculos muy rápido. Sin embargo, la racionalización sigue siendo una herramienta útil en matemáticas para simplificar expresiones y entender mejor cómo funcionan los números. Es como ordenar una habitación para que sea más fácil de usar.
Tipos de racionalización
Existen diferentes maneras de racionalizar, dependiendo de cómo sea la expresión con la raíz en el denominador.
Racionalización simple: Cuando hay una sola raíz cuadrada
Cuando el denominador es una sola raíz cuadrada (un monomio), el proceso es bastante directo.
Por ejemplo, si tenemos la fracción:
Para quitar la raíz cuadrada de 5 del denominador, multiplicamos tanto el numerador como el denominador por 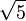 . Es como multiplicar por 1, así que la fracción no cambia su valor:
. Es como multiplicar por 1, así que la fracción no cambia su valor:
Sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (\sqrt{5})^2 es igual a 5. Así, la raíz desaparece del denominador:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{{8\sqrt{5}}}{{(\sqrt{5})}^2} = \frac{8\sqrt{5}}{5}
¡Y listo! Ahora el denominador es un número entero, sin raíces.
Racionalización de binomios: Cuando hay sumas o restas de raíces
Cuando el denominador tiene una suma o resta de dos términos, y al menos uno de ellos es una raíz cuadrada, usamos un truco especial llamado "binomio conjugado".
El binomio conjugado de una expresión como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A + B es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A - B . Y el conjugado de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A - B es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A + B . Cuando multiplicamos un binomio por su conjugado, las raíces suelen desaparecer.
Veamos un ejemplo:
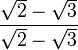
El conjugado del denominador Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{2}+\sqrt{3} es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{2}-\sqrt{3} . Multiplicamos el numerador y el denominador por este conjugado:
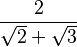 ·
· 
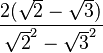
Al multiplicar los denominadores, usamos una regla de los productos notables que dice que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a+b)(a-b) = a^2 - b^2 :
Ahora, simplificamos los cuadrados de las raíces:
Y resolvemos la resta en el denominador:
Finalmente, podemos mover el signo negativo al numerador:
¡Hemos quitado las raíces del denominador!
Racionalización de monomios con índices mayores a dos
A veces, tenemos raíces que no son cuadradas, como raíces cúbicas (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt[3]{} ), raíces quintas (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt[5]{} ), etc. El proceso es un poco diferente.
Considera este caso:
Primero, reescribimos el número 8 como una potencia de 2:
Para eliminar la raíz quinta, necesitamos que los exponentes de los términos dentro de la raíz sean múltiplos de 5 (el índice de la raíz).
- Para
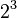 , necesitamos
, necesitamos 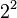 para llegar a
para llegar a 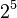 .
. - Para
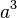 , necesitamos
, necesitamos 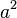 para llegar a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^5 .
para llegar a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^5 . - Para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^4 , necesitamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^1 (o simplemente
 ) para llegar a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^5 .
) para llegar a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^5 .
Entonces, la expresión por la que multiplicaremos el numerador y el denominador es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt[5]{2^2a^2b} :
![\frac{{2}}{\sqrt[5]{2^3a^3b^4}}](/images/math/8/1/a/81a07829eb2a526acc5c99c442f8095e.png) ·
· ![\frac{\sqrt[5]{2^2a^2b} }{\sqrt[5]{2^2a^2b}}](/images/math/8/9/3/89315c6b50c3027d25e1f1e95b61d6fd.png)
Multiplicamos los términos dentro de las raíces en el denominador:
Ahora, como los exponentes son iguales al índice de la raíz, podemos sacar los términos de la raíz:
Finalmente, simplificamos el 2 del numerador y el 2 del denominador:
Racionalización de binomios con radical mayor a dos
Cuando tenemos sumas o restas de raíces cúbicas en el denominador, usamos otras reglas de productos notables.
Si tenemos una diferencia de raíces cúbicas, como:
Usamos la regla Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^3 - y^3 = (x-y)(x^2 + xy + y^2) . Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = \sqrt[3]{a} y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = \sqrt[3]{b} . Multiplicamos por el segundo factor:
![\frac{{1}}{\sqrt[3]{a}-\sqrt[3]{b}}](/images/math/b/4/b/b4bb468eebe86398e4e66a6e93c2d59b.png) ·
· ![\frac{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}](/images/math/4/d/b/4db68097063d35de990bc5bc351317a7.png)
El denominador se convierte en  :
:
Si tenemos una suma de raíces cúbicas:
Usamos la regla Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^3 + y^3 = (x+y)(x^2 - xy + y^2) . Multiplicamos por el segundo factor:
![\frac{{1}}{\sqrt[3]{a}+\sqrt[3]{b}}](/images/math/a/d/7/ad73cd42e1ec501d51debc522d65ae4e.png) ·
· ![\frac{\sqrt[3]{a^2} - \sqrt[3]{ab}+ \sqrt[3]{b^2}}{\sqrt[3]{a^2} - \sqrt[3]{ab}+ \sqrt[3]{b^2}}](/images/math/1/4/b/14bdef45342c41b2adcd4eef79c88ae5.png)
El denominador se convierte en  :
:
Véase también
 En inglés: Rationalisation (mathematics) Facts for Kids
En inglés: Rationalisation (mathematics) Facts for Kids


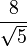
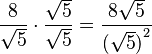
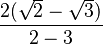
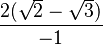
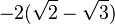
![\frac{{2}}{\sqrt[5]{8a^3b^4}}](/images/math/2/8/b/28b560d173a879a45f5a697d212ec501.png)
![\frac{{2\sqrt[5]{2^2a^2b}}}{\sqrt[5]{2^5a^5b^5}}](/images/math/e/3/9/e393322e7e2301bdd0c26b9df0405992.png)
![\frac{{2\sqrt[5]{4a^2b}}}{{2ab}}](/images/math/1/5/7/157186c3d733b0a6317bfe11b3bbd31a.png)
![\frac{{\sqrt[5]{4a^2b}}}{{ab}}](/images/math/a/a/4/aa4f5f2ff57625eeecb4f8ca585d8d45.png)
![\frac{{\sqrt[3]{a^2} + \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{{a}-{b}}}](/images/math/0/4/4/0443828f1f2149056f91096297979fe4.png)
![\frac{{\sqrt[3]{a^2} - \sqrt[3]{ab}+ \sqrt[3]{b^2}}}{{{a}+{b}}}](/images/math/4/d/f/4df6bad8e9abd716cffd1f0e78527815.png)