Proyección ortogonal para niños

En geometría euclidiana, la proyección ortogonal es una forma especial de "dibujar" una figura sobre una línea o un plano. Imagina que tienes una linterna y la apuntas directamente hacia una pared. La sombra que se forma en la pared es una proyección ortogonal de lo que sea que estés iluminando. En matemáticas, esto significa que las líneas que usamos para proyectar son siempre perpendiculares (forman un ángulo de 90 grados) a la línea o plano donde se proyecta la figura.

En un plano, la proyección ortogonal ocurre cuando las líneas que usamos para proyectar son perpendiculares a una línea de referencia, a la que llamamos L. Por ejemplo, si tienes un segmento de línea llamado AB, solo necesitas proyectar sus puntos finales (A y B) sobre la línea L usando líneas perpendiculares. Así, obtendrás un nuevo segmento que es la proyección de AB sobre L.

Este concepto es muy útil en matemáticas y física. Por ejemplo, se usa en los teoremas de las relaciones métricas en el triángulo para calcular las medidas de los lados de un triángulo. La idea de proyección ortogonal se puede aplicar no solo en un plano, sino también en espacios con muchas más dimensiones.

¿Cómo se Proyecta Ortogonalmente?

Proyectar un Punto en una Línea

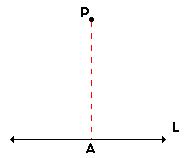
Cuando queremos proyectar un punto P sobre una línea L, el resultado es otro punto, al que llamamos A. Para encontrar A, dibujamos una línea auxiliar que sale de P y es completamente perpendicular a L. El punto donde esta línea auxiliar toca a L es A. Si el punto P ya está sobre la línea L, entonces su proyección es el mismo punto P.

La proyección del punto P sobre la línea L es el punto A.

Proyectar un Segmento en una Línea

Proyectar un segmento de línea es similar a proyectar un punto, pero lo hacemos con los dos extremos del segmento.

Segmento no Paralelo a la Línea

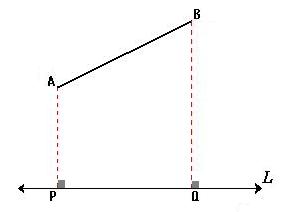
Si el segmento AB no es paralelo a la línea L, su proyección ortogonal será un segmento más corto, al que llamamos PQ. Para encontrar PQ, dibujamos líneas perpendiculares desde los puntos A y B hasta la línea L. Los puntos donde estas líneas tocan a L son P y Q. La longitud de PQ siempre será menor que la de AB.

La proyección del segmento AB sobre la línea L es el segmento PQ.

Segmento Paralelo a la Línea

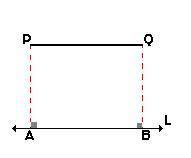
Si el segmento AB es paralelo a la línea L, su proyección PQ tendrá la misma longitud que AB. Se obtiene de la misma manera, dibujando líneas perpendiculares desde los extremos de AB hasta L. En este caso, AB es igual a PQ.

Si el segmento es paralelo a la línea, su proyección tiene la misma longitud.

Segmento con un Punto en la Línea

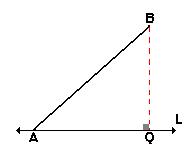
Si uno de los puntos del segmento AB ya está sobre la línea L (por ejemplo, el punto A), entonces la proyección de A es el mismo punto A. Solo necesitamos proyectar el otro punto, B, sobre L para encontrar Q. La proyección del segmento será AQ.

Cuando un extremo del segmento está en la línea.

Segmento que Corta la Línea

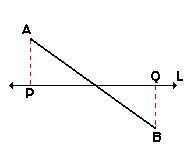
Si el segmento AB cruza la línea L, la proyección se encuentra de la misma forma. Proyectamos los puntos A y B sobre L para obtener P y Q. La proyección del segmento será PQ.

Cuando el segmento cruza la línea.

Véase también

En inglés: Orthographic projection Facts for Kids

• Relaciones métricas en el triángulo