Proceso de ortogonalización de Gram-Schmidt para niños
El proceso de Gram-Schmidt es una herramienta matemática muy útil que nos ayuda a transformar un grupo de vectores en otro grupo de vectores que son especiales: todos son perpendiculares entre sí. Imagina que tienes varias flechas en el espacio que apuntan en diferentes direcciones. Con este proceso, puedes convertirlas en un nuevo conjunto de flechas que forman ángulos de 90 grados entre sí, como las esquinas de una habitación.
Este método lleva el nombre de dos matemáticos, Jørgen Pedersen Gram y Erhard Schmidt, quienes contribuyeron a su desarrollo.
Contenido
¿Qué es el proceso de Gram-Schmidt?
El proceso de Gram-Schmidt se utiliza para encontrar "bases ortogonales" o "bases ortonormales". En matemáticas, una "base" es un conjunto de vectores que pueden usarse para construir cualquier otro vector en un espacio.
- Una base es ortogonal si todos sus vectores son perpendiculares entre sí. Piensa en los ejes X, Y y Z de un gráfico tridimensional: son perpendiculares.
- Una base es ortonormal si, además de ser ortogonal, cada vector tiene una "longitud" o "magnitud" de 1. Esto significa que están "normalizados".
Este proceso es muy útil en áreas como la física, la ingeniería y la informática, especialmente cuando se trabaja con datos o gráficos en múltiples dimensiones.
¿Cómo funciona el algoritmo de Gram-Schmidt?
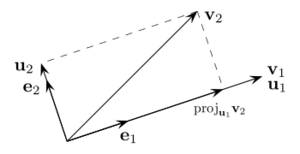
La idea principal del proceso de Gram-Schmidt se basa en un concepto de la geometría euclídea: si tienes un vector y le restas su "proyección" sobre otro vector, el resultado es un nuevo vector que es perpendicular al segundo.
Imagina que tienes un vector v y otro vector u. La "proyección" de v sobre u es como la sombra que v proyectaría sobre u si la luz viniera de arriba. Si restas esa sombra a v, lo que queda es un vector que es perpendicular a u.
El algoritmo funciona paso a paso:
- Se toma el primer vector del conjunto original y se convierte en el primer vector del nuevo conjunto.
- Para el segundo vector, se le resta su proyección sobre el primer vector del nuevo conjunto. Esto asegura que el nuevo segundo vector sea perpendicular al primero.
- Para el tercer vector, se le restan sus proyecciones sobre los dos primeros vectores del nuevo conjunto. Así, el nuevo tercer vector será perpendicular a los dos anteriores.
- Este proceso se repite para todos los vectores del conjunto original.
Al final, obtendrás un nuevo conjunto de vectores donde todos son perpendiculares entre sí. Si además quieres que cada vector tenga una longitud de 1, solo tienes que dividir cada vector por su propia longitud.
Ejemplos prácticos del proceso
Veamos cómo funciona con algunos ejemplos sencillos.
- Ejemplo 1: Dos vectores en un plano
Imagina que tienes dos vectores en un plano (como un dibujo en una hoja de papel): * v1 = (2, 1) * v2 = (1, 4)
Queremos encontrar dos nuevos vectores, u1 y u2, que sean perpendiculares.
1. El primer vector u1 es igual al primer vector original: u1 = v1 = (2, 1)
2. Para encontrar u2, restamos la proyección de v2 sobre u1: La proyección de v2 sobre u1 es (12/5, 6/5). Entonces, u2 = v2 - Proyección = (1, 4) - (12/5, 6/5) = (-7/5, 14/5).
Ahora, los vectores (2, 1) y (-7/5, 14/5) son perpendiculares entre sí. Puedes comprobarlo multiplicando sus componentes y sumando los resultados: (2 * -7/5) + (1 * 14/5) = -14/5 + 14/5 = 0. Cuando el resultado es 0, significa que son perpendiculares.
- Ejemplo 2: Tres vectores en el espacio
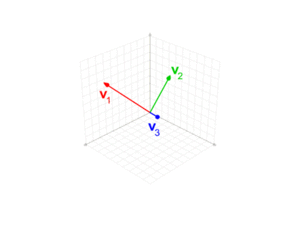
Ahora, con tres vectores en un espacio tridimensional: * v1 = (2, 1, 1) * v2 = (1, 0, 10) * v3 = (2, -3, 11)
1. u1 = v1 = (2, 1, 1)
2. Calculamos u2: Proyección de v2 sobre u1 = (4, 2, 2). u2 = v2 - Proyección = (1, 0, 10) - (4, 2, 2) = (-3, -2, 8).
3. Calculamos u3: Proyección de v3 sobre u1 = (4, 2, 2). Proyección de v3 sobre u2 = (-24/7, -16/7, 64/7). u3 = v3 - Proyección(v3 sobre u1) - Proyección(v3 sobre u2) u3 = (2, -3, 11) - (4, 2, 2) - (-24/7, -16/7, 64/7) = (10/7, -19/7, -1/7).
Así, obtenemos el conjunto de vectores perpendiculares: * u1 = (2, 1, 1) * u2 = (-3, -2, 8) * u3 = (10/7, -19/7, -1/7)
Estos nuevos vectores forman una base ortogonal, lo que significa que son perpendiculares entre sí.
Galería de imágenes
Véase también
 En inglés: Gram–Schmidt process Facts for Kids
En inglés: Gram–Schmidt process Facts for Kids