Paradoja de Hooper para niños
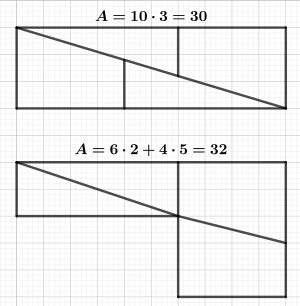
La paradoja de Hooper es un truco visual muy interesante que parece desafiar la lógica, pero en realidad es una ilusión óptica. Imagina que tienes una figura geométrica con un área de 32 unidades. Esta figura se divide en cuatro piezas. Luego, estas piezas se reacomodan para formar un rectángulo que, sorprendentemente, ¡parece tener un área de solo 30 unidades! La "paradoja" es que 2 unidades de área parecen haber desaparecido.
Contenido
¿Cómo funciona la paradoja de Hooper?
Si observas con mucho cuidado, te darás cuenta de que los triángulos que se usan en la figura original no son exactamente iguales a los triángulos que forman el rectángulo. Por ejemplo, el lado más corto de los triángulos en la figura original mide 2 unidades. Sin embargo, cuando se usan para formar el rectángulo, ese mismo lado parece medir solo 1.8 unidades.
El secreto de la ilusión
Esto significa que los triángulos de la figura original se superponen un poco cuando se colocan en el rectángulo. El espacio donde se superponen forma una figura llamada paralelogramo. Este paralelogramo es el "área perdida" que hace que la paradoja funcione.
Calculando el área "desaparecida"
El área de este paralelogramo se puede calcular usando fórmulas matemáticas. Si se hacen los cálculos correctamente, se descubre que el área de este paralelogramo es exactamente 2 unidades. ¡Así que las 2 unidades de área no desaparecieron, sino que se convirtieron en un espacio superpuesto dentro de la nueva figura!
Historia de la paradoja de Hooper
Esta curiosa paradoja fue publicada por William Hooper en el año 1774. Apareció en su libro llamado Rational Recreations. Hooper la llamó "El dinero geométrico".
Orígenes y correcciones
La primera edición de su libro, la de 1774, tenía un dibujo que no era del todo correcto. Sin embargo, este error se arregló en la edición de 1782. Es importante saber que Hooper no fue el primero en mostrar este tipo de truco geométrico. Su libro se basó en gran parte en otro libro anterior, Nouvelles récréations physiques et mathétiques, escrito por Edmé-Gilles Guyot y publicado en Francia en 1769. El libro de Guyot también tenía el mismo dibujo incorrecto al principio, que luego fue corregido en ediciones posteriores.
Véase también
 En inglés: Hooper's paradox Facts for Kids
En inglés: Hooper's paradox Facts for Kids