Operador de proyección para niños

Un operador de proyección en matemáticas es como una herramienta especial que toma un punto o un vector y lo "lanza" o "proyecta" sobre un espacio más pequeño, como una sombra en una pared. Imagina que tienes una linterna y proyectas la sombra de un objeto sobre una superficie plana. El operador de proyección hace algo similar, pero con números y formas matemáticas.

Lo más importante de un operador de proyección, que llamamos P, es que si lo aplicas dos veces, obtienes el mismo resultado que si lo aplicaras una sola vez. Esto se conoce como ser idempotente, y se escribe como P² = P.

¿Qué es un Operador de Proyección?

Estos operadores "proyectan" cualquier punto de un espacio matemático a un punto dentro de un subespacio (una parte más pequeña de ese espacio). Si el punto ya está en ese subespacio, el operador no hace nada, lo deja exactamente donde está.

Por ejemplo, piensa en un punto en el espacio tridimensional, como (x, y, z). Un operador de proyección podría transformarlo en (x, 0, z). Esto es como proyectar el punto sobre el plano donde la coordenada 'y' es cero. Es decir, la sombra del punto se vería en el plano XZ.

Esta idea de "proyectar" se usa en matemáticas para muchos tipos de espacios, incluso aquellos que no podemos dibujar fácilmente.

¿Cómo se Descompone un Vector con una Proyección?

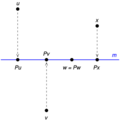
Imagina que tienes un vector (una flecha) en un espacio. Un operador de proyección P puede dividir este vector en dos partes. Una parte es la proyección del vector (la "sombra"), y la otra es lo que queda después de la proyección.

Si llamamos I al operador que no cambia nada (la identidad), entonces si P es una proyección, el operador Q = I - P también es una proyección. Esto significa que cualquier vector x se puede escribir como la suma de su proyección P(x) y la proyección de lo que queda Q(x).

Proyecciones Ortogonales: Cuando las Sombras son Perpendiculares

Para entender las "proyecciones ortogonales", necesitamos saber qué significa que dos vectores sean ortogonales, que es lo mismo que decir que son perpendiculares entre sí. Para saber si son perpendiculares, usamos algo llamado "producto interior" (o producto escalar).

Una proyección ortogonal es un tipo especial de proyección donde la "sombra" que se crea es perpendicular a la dirección desde la que se proyecta. Es como si la luz viniera directamente de arriba, creando una sombra que forma un ángulo de 90 grados con la superficie.

En física, cuando se habla de "operador de proyección", casi siempre se refieren a una proyección ortogonal.

Ejemplos de Proyecciones

Proyección Ortogonal en un Plano

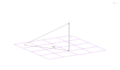
Un ejemplo sencillo es proyectar un punto (x, y, z) en el espacio tridimensional sobre el plano XY. El punto se convierte en (x, y, 0). Esto es como si el punto se aplastara sobre el suelo.

Esta operación se puede representar con una matriz: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}. Cuando aplicas esta matriz a un vector, obtienes: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} x \\ y \\ 0 \end{bmatrix}. Si aplicas P dos veces, verás que el resultado es el mismo que aplicarlo una vez, lo que confirma que es una proyección. Además, esta es una proyección ortogonal porque la matriz P es igual a su transpuesta (cuando sus filas y columnas se intercambian).

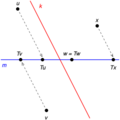
Proyección Oblicua: Sombras Inclinadas

Una proyección oblicua es cuando la "sombra" no es perpendicular a la dirección de proyección. Imagina que la luz viene de lado, creando una sombra alargada o inclinada.

Un ejemplo de matriz para una proyección oblicua es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P= \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix}. Si calculas P², verás que es igual a P, así que es una proyección. Sin embargo, solo es ortogonal si el valor de es 0. Si no es 0, la proyección es oblicua.

Propiedades de los Operadores de Proyección

Idempotencia

Como ya mencionamos, la propiedad principal de una proyección P es que es idempotente: P² = P. Esto significa que aplicar la proyección una vez es suficiente; aplicarla más veces no cambia el resultado.

Imagen y Núcleo Complementarios

Cada proyección P divide el espacio en dos partes:

• La imagen de P: Son todos los puntos que resultan de la proyección. Si un punto ya está en la imagen, P lo deja igual.
• El núcleo de P: Son todos los puntos que la proyección convierte en cero.

Estas dos partes son "complementarias", lo que significa que juntas forman el espacio completo, y solo tienen el punto cero en común.

Valores Propios

Los "valores propios" de una proyección solo pueden ser 0 o 1. Esto significa que cuando una proyección actúa sobre un vector, o lo deja igual (si es 1) o lo convierte en cero (si es 0).

Producto de Proyecciones

Si multiplicas dos proyecciones, el resultado no siempre es otra proyección. Sin embargo, si las dos proyecciones "conmutan" (es decir, el orden en que las aplicas no importa), entonces su producto sí es una proyección.

Fórmulas para Proyecciones Ortogonales

Cuando la proyección ortogonal es sobre una línea recta, y tienes un vector unitario (de longitud 1) u en esa línea, la proyección se puede calcular con una fórmula sencilla.

Si tienes una base de vectores ortonormales (perpendiculares y de longitud 1) para un subespacio, puedes construir una matriz A con esos vectores. La proyección sobre ese subespacio se calcula como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_A= A A^\mathsf{T} Donde A^T es la matriz transpuesta de A.

Si los vectores de la base no son ortonormales, la fórmula es un poco más compleja: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_A= A \left(A^\mathsf{T} A\right)^{-1} A^\mathsf{T}. Aquí, (A^TA)^-1 es la inversa de la multiplicación de A transpuesta por A.

Aplicaciones de los Operadores de Proyección

Los operadores de proyección son muy importantes en muchas áreas de las matemáticas y la ciencia, incluyendo:

• Factorización QR: Un método para descomponer matrices.
• Regresión lineal: Una técnica estadística para encontrar la relación entre variables.
• Aprendizaje automático: Se usan para encontrar la distancia más corta entre un punto y un espacio.

En general, las proyecciones son herramientas fundamentales en el estudio de los espacios vectoriales y tienen muchas aplicaciones prácticas en campos como la ingeniería, la física y la informática.

Galería de imágenes

• 

  La transformación P es la proyección ortogonal sobre una recta m

• 

  y proyectado en el espacio vectorial V

• 

  La transformación T es la proyección a lo largo de k sobre m. El rango de T es m y el núcleo es k

Véase también

En inglés: Parallel projection Facts for Kids