Número de Carmichael para niños
Los números de Carmichael son un tipo especial de números compuestos que, a primera vista, parecen ser números primos cuando se les aplica una prueba matemática específica. Reciben su nombre del matemático Robert Daniel Carmichael, quien los estudió.
Contenido
Números de Carmichael: ¿Qué son?
En matemáticas, un número primo es un número entero mayor que 1 que solo puede dividirse exactamente por 1 y por sí mismo (como 2, 3, 5, 7...). Un número compuesto es un número entero mayor que 1 que tiene más de dos divisores (como 4, 6, 8, 9...).
Los números de Carmichael son compuestos, pero tienen una característica muy particular: se comportan como si fueran primos en una prueba matemática llamada el Pequeño Teorema de Fermat. Esto significa que pueden "engañar" a algunas pruebas que se usan para saber si un número es primo o no.
¿Por qué son especiales los números de Carmichael?
La razón por la que los números de Carmichael son especiales es que cumplen una condición matemática que normalmente solo cumplen los números primos. Esta condición se expresa así:

Esto significa que si tomas un número a (que no comparte divisores con n más allá del 1, es decir, son primos relativos), lo elevas a la potencia de n-1, y luego divides el resultado por n, el resto siempre será 1. Los números primos siempre cumplen esto, pero los números de Carmichael también lo hacen, a pesar de ser compuestos.
El Pequeño Teorema de Fermat: La base de todo
Para entender mejor a los números de Carmichael, necesitamos conocer el Pequeño Teorema de Fermat. Este teorema dice que si p es un número primo, entonces la siguiente relación es verdadera:
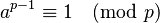
Esto se cumple para cualquier número a que no sea divisible por p. En otras palabras, si a no es un múltiplo de p, entonces p siempre dividirá a ap-1-1 sin dejar resto.
¿Cómo nos engañan los números de Carmichael?
Normalmente, para saber si un número n es primo, se puede usar una prueba basada en el Teorema de Fermat. Se elige un número a que sea primo relativo con n y se calcula si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{n-1}\pmod n es igual a 1.
- Si el resultado es diferente de 1, ¡entonces sabemos con seguridad que n es un número compuesto!
- Pero si el resultado es 1, aquí está el problema: no podemos estar 100% seguros de que n sea primo. Esto se debe a que existen números compuestos que también cumplen esta condición. A estos números se les llama pseudoprimos en la base a.
Los números de Carmichael son el caso más extremo de pseudoprimos: son números compuestos que cumplen la condición del Teorema de Fermat para cualquier número a que sea primo relativo con ellos. Por eso, la prueba de Fermat "falla" con ellos, ya que los confunde con números primos.
Ejemplos de números de Carmichael
Los primeros números de Carmichael son:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973, 75361\ldots
El primer número de Carmichael es el 561. Podemos ver que es un número compuesto porque se puede escribir como la multiplicación de otros números:
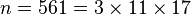
A pesar de ser compuesto, si tomas cualquier número a que no sea divisible por 3, 11 o 17, y calculas Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{560}-1 , el resultado siempre será divisible por 561.
Véase también
 En inglés: Carmichael number Facts for Kids
En inglés: Carmichael number Facts for Kids
- Pseudoprimo
- Introducción a la Matemática Discreta

