Método de los elementos finitos para niños

Visualización de una simulación del MEF que muestra cómo se deforma un coche después de un choque frontal.

Una solución del MEF en 2D para un imán. Las líneas muestran la dirección del flujo calculado y el color, su fuerza.

Una malla 2D, que es como una red de puntos. La malla es más densa donde se necesita más detalle.

Una función (azul) y su aproximación lineal (rojo) en el MEF.

Triangulación, que es como dividir una forma grande en muchos triángulos pequeños.

El Método de los Elementos Finitos (MEF) es una herramienta matemática muy útil que se usa en computadoras para resolver problemas complejos de ingeniería y física. Imagina que tienes un problema muy grande, como saber cómo se dobla un puente bajo el peso de los coches o cómo fluye el calor a través de una ventana. El MEF ayuda a encontrar soluciones aproximadas para estos desafíos.

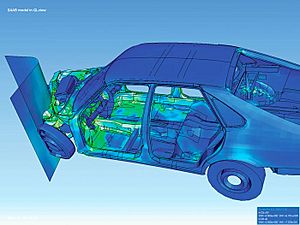
Este método es muy importante en el diseño y la mejora de productos, desde coches y aviones hasta edificios y dispositivos electrónicos. También se usa para simular cómo funcionan sistemas físicos y biológicos complicados. Su gran ventaja es que puede trabajar con formas y diseños muy elaborados, algo que sería casi imposible de calcular a mano.

¿Qué es el Método de los Elementos Finitos?

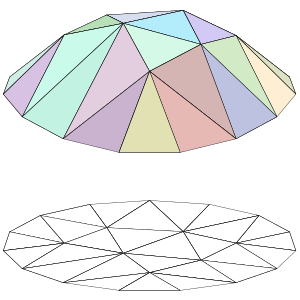
El MEF nos permite encontrar una solución numérica aproximada para el comportamiento de un objeto o una estructura. Para lograrlo, el método divide el objeto grande en muchas partes más pequeñas que no se superponen, llamadas "elementos finitos". Piensa en ello como si cortaras un pastel en muchas rebanadas pequeñas.

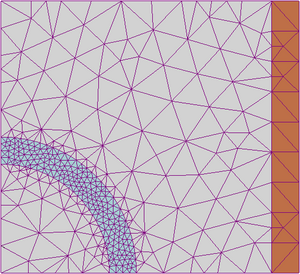
Cada uno de estos elementos finitos tiene puntos especiales llamados "nodos". Si dos nodos están cerca y pertenecen al mismo elemento, se dice que son "adyacentes". El conjunto de todos estos nodos y sus conexiones forma lo que se conoce como una "malla".

Los cálculos se hacen sobre esta malla de puntos. Para crear la malla, se usan programas especiales antes de empezar los cálculos. Una vez que tenemos la malla, el método relaciona los valores de las incógnitas (como el movimiento o la temperatura) en cada nodo. Estas relaciones se convierten en un gran sistema de ecuaciones que la computadora puede resolver. Cuantos más nodos y elementos tenga la malla, más precisa será la solución, pero también tomará más tiempo calcularla.

El MEF es muy popular porque es muy versátil. Se puede usar para entender cómo se mueven y deforman los materiales, cómo se transmite el calor, cómo fluyen los líquidos (esto se llama mecánica de fluidos computacional) o cómo se comportan los campos eléctricos y magnéticos. Como es muy difícil encontrar soluciones exactas para estos problemas en la vida real, el MEF se convierte en la mejor opción para los ingenieros.

Historia del MEF

El Método de los Elementos Finitos empezó a desarrollarse en 1943 gracias a Richard Courant. Él usó una técnica matemática para encontrar soluciones aproximadas a problemas de vibración. Más tarde, en 1956, un grupo de ingenieros (M. J. Turner, R. W. Clough, H. C. Martin y L. J. Topp) publicaron un trabajo que amplió la idea, enfocándose en cómo se comportan las estructuras complejas.

Los primeros pasos del MEF (1950-1970)

Cuando llegaron las primeras computadoras en la década de 1950, el cálculo de estructuras era un trabajo muy largo y manual. Calcular un edificio de varios pisos podía llevar semanas. Las computadoras cambiaron esto por completo. Permitieron usar métodos que antes eran demasiado complicados porque requerían resolver sistemas de ecuaciones enormes.

En los años 60, a medida que las aplicaciones del MEF crecían, se hizo necesario que los cálculos fueran más rápidos y eficientes. Se mejoraron los algoritmos para resolver los sistemas de ecuaciones, lo que ahorró mucho tiempo. Esto hizo que el método se extendiera rápidamente, especialmente en el diseño de edificios.

Sin embargo, todavía era difícil aplicar el MEF a formas muy complejas o a objetos continuos como superficies y volúmenes. Por eso, las nuevas técnicas del MEF comenzaron a desarrollarse en el campo aeroespacial, donde se necesitaban soluciones para diseños de aviones y cohetes. El método también se aplicó a otros campos como la transmisión de calor y la mecánica de fluidos.

En los años 60, con la aparición de los primeros programas comerciales, el MEF se hizo popular en la industria y sus bases teóricas se fortalecieron en las universidades. En los años 70, la cantidad de libros y estudios sobre el MEF creció mucho, y el método se extendió a problemas más complejos. En esa época, el MEF solo estaba disponible en computadoras muy caras, usadas principalmente por las industrias aeronáutica, automotriz, de defensa y nuclear.

El MEF en la era de las computadoras personales (Desde 1980)

Estructura generada por el MEF para analizar las fuerzas en la cabeza de un pistón de motor.

A partir de los años 80, con la llegada de las computadoras personales, el uso de programas comerciales de MEF se hizo mucho más común. Estos programas incluían herramientas gráficas para crear las mallas y mostrar los resultados de forma visual. Se siguió investigando cómo aplicar el método a nuevos tipos de materiales y comportamientos, y cómo analizar los posibles errores.

Hoy en día, el MEF es una herramienta fundamental. Gracias a la disminución del costo de las computadoras y al enorme aumento de su capacidad de cálculo, el MEF ha logrado una precisión increíble. Las supercomputadoras actuales pueden dar resultados muy exactos para casi cualquier tipo de problema.

¿Cómo trabaja el MEF en la práctica?

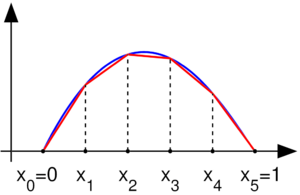
El MEF es un método numérico que resuelve ecuaciones complejas. La solución que se obtiene es una aproximación, lo que significa que es muy cercana a la solución real, pero no exactamente igual, excepto en los puntos llamados "nodos". En los puntos que no son nodos, la solución se calcula interpolando (estimando) a partir de los resultados de los nodos.

El MEF transforma un problema de ecuaciones complejas en un problema de matrices que la computadora puede resolver. El proceso se divide en tres etapas principales:

Preparación (Preproceso)

En esta etapa, se define la forma del objeto, se crea la malla (la red de puntos y elementos) y se le dice al programa qué tipo de material es y qué condiciones se le aplicarán (por ejemplo, dónde se apoya o dónde se le aplica una fuerza). La malla puede tener miles de puntos. Las zonas donde se espera que haya más fuerza o cambios importantes suelen tener más nodos para que el cálculo sea más preciso.

Cálculo

Una vez que la malla y las condiciones están listas, el programa resuelve el sistema de ecuaciones. Si el problema es sencillo y no cambia con el tiempo, el cálculo es directo. Pero si el problema es más complejo, como cuando las fuerzas cambian mucho o el objeto se deforma de manera no lineal, el cálculo se hace en pequeños pasos. En cada paso, se resuelve un sistema de ecuaciones, y el resultado de un paso afecta al siguiente. Estos problemas más complejos requieren mucho más tiempo de cálculo.

Análisis de Resultados (Postproceso)

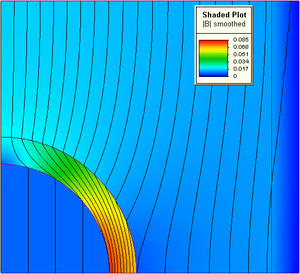
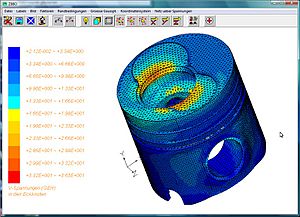
Después de que la computadora termina los cálculos, los resultados son una gran cantidad de números. En la etapa de postproceso, estos números se transforman en gráficos y visualizaciones que son fáciles de entender. Por ejemplo, se pueden ver mapas de colores que muestran dónde hay más fuerza o calor en el objeto. Esto ayuda a los ingenieros a interpretar los resultados y a decidir si el diseño es seguro o si necesita mejoras.

Tipos de problemas que resuelve el MEF

El MEF puede resolver una gran variedad de problemas, como:

• Calcular la masa, el volumen o la temperatura de un objeto.
• Determinar las fuerzas, el movimiento, la velocidad o la aceleración.
• Analizar cómo se comporta un material bajo diferentes tipos de carga (como peso, presión, calor o fuerzas de giro).

Los programas de MEF tienen una biblioteca de "elementos" que se pueden usar para construir la malla, como:

• Elementos tipo barra (para estructuras largas y delgadas).
• Elementos tipo viga (para soportes).
• Elementos de placa o cáscara (para superficies delgadas).
• Elementos sólidos (para objetos tridimensionales).
• Elementos de muelle o amortiguador (para simular elasticidad o absorción de impactos).

También pueden simular diferentes tipos de materiales, como:

• Materiales elásticos (que vuelven a su forma original después de deformarse).
• Materiales homogéneos (uniformes en todas partes) o heterogéneos (con diferentes propiedades).
• Materiales que se deforman permanentemente (plasticidad) o que cambian con el tiempo (viscosidad).

Métodos Implícitos y Explícitos

En problemas donde las cosas cambian con el tiempo (problemas dinámicos), el MEF divide el tiempo en pequeños intervalos. Hay dos formas principales de hacer esto:

El Método Implícito

Este método requiere resolver un sistema de ecuaciones en cada pequeño paso de tiempo. Aunque esto puede tomar más tiempo por cada paso, permite usar intervalos de tiempo más grandes, lo que a veces hace que el cálculo total sea más rápido y estable. Se usa mucho para calcular la rigidez de las estructuras.

El Método Explícito

Este método no necesita resolver un sistema de ecuaciones en cada paso de tiempo, lo que lo hace más rápido por cada intervalo. Sin embargo, para que los resultados sean estables y precisos, los pasos de tiempo deben ser muy pequeños. Se usa mucho para simular eventos rápidos, como choques o explosiones, donde hay cambios muy grandes y repentinos. Una ventaja es que se puede dividir el trabajo entre varias computadoras, lo que acelera el cálculo.

Programas que utilizan el método de elementos finitos

|

Véase también

En inglés: Finite element method Facts for Kids