Método de bisección para niños
En matemáticas, el método de bisección, también conocido como dicotomía, es una forma de encontrar las "raíces" de una función. Una raíz es el punto donde la gráfica de una función cruza el eje horizontal (el eje X), es decir, donde el valor de la función es cero. Este método funciona dividiendo un intervalo (un rango de números) a la mitad una y otra vez, hasta encontrar el punto donde la función es cero.
Contenido
¿Qué es el Método de Bisección?
El método de bisección es una herramienta matemática que nos ayuda a resolver ecuaciones de una manera sencilla. Imagina que tienes una ecuación como f(x) = 0 y quieres saber qué valor de x hace que esa ecuación sea verdadera. El método de bisección te ayuda a encontrar ese valor.
También se le conoce como el "Método del Intervalo Medio" porque su idea principal es siempre dividir un intervalo por la mitad. Es uno de los métodos más fáciles de entender y usar para encontrar soluciones a ecuaciones.
¿Cómo Funciona? El Teorema del Valor Intermedio
El método de bisección se basa en una idea importante llamada el Teorema del Valor Intermedio (TVI). Para entenderlo, piensa en una función continua. Una función continua es como una línea o curva que puedes dibujar en un papel sin levantar el lápiz. No tiene saltos ni huecos.
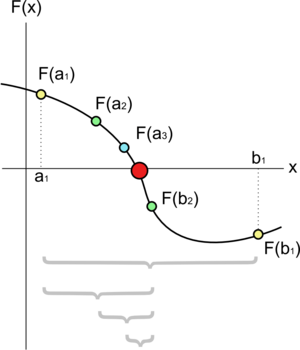
El Teorema del Valor Intermedio dice lo siguiente: si tienes una función continua en un intervalo (por ejemplo, desde un punto 'a' hasta un punto 'b'), y si el valor de la función en 'a' (f(a)) y el valor de la función en 'b' (f(b)) tienen signos opuestos (uno es positivo y el otro es negativo), entonces la función debe cruzar el cero en algún lugar dentro de ese intervalo. Es decir, ¡debe haber una raíz allí!
Pasos para Encontrar una Raíz
El método de bisección sigue estos pasos:
- Primero, asegúrate de que la función sea continua en el intervalo que elegiste, digamos de 'a' a 'b'.
- Luego, verifica que los valores de la función en los extremos del intervalo, f(a) y f(b), tengan signos diferentes. Si uno es positivo y el otro negativo, ¡sabes que hay una raíz entre ellos!
- Calcula el punto medio del intervalo. Llamémoslo 'm'. Es decir, m = (a + b) / 2.
- Ahora, calcula el valor de la función en ese punto medio, f(m).
- Si f(m) es igual a cero, ¡felicidades! Has encontrado la raíz.
- Si f(m) no es cero, mira su signo.
* Si f(m) tiene un signo diferente al de f(a), significa que la raíz está en el nuevo intervalo [a, m]. * Si f(m) tiene un signo diferente al de f(b), entonces la raíz está en el nuevo intervalo [m, b].
- Ahora, el nuevo intervalo es más pequeño. Repite todos los pasos con este nuevo intervalo.
- Continúa haciendo esto una y otra vez. Cada vez, el intervalo se hace más pequeño, "encerrando" la raíz hasta que encuentres una solución con la precisión que necesitas.
Ventajas y Desventajas
El método de bisección es muy confiable. Si las condiciones iniciales se cumplen (la función es continua y los valores en los extremos tienen signos opuestos), ¡siempre encontrarás una raíz! Esto lo hace muy seguro.
Sin embargo, no es el método más rápido. Otros métodos, como el método de Newton, pueden encontrar la raíz más rápidamente. Pero el método de bisección garantiza que siempre llegará a una solución, aunque sea un poco más lento.
La precisión de la solución mejora con cada paso. Después de 'n' pasos, el error máximo que puedes tener es la longitud del intervalo inicial dividida por 2 elevado a la potencia 'n'. Esto significa que el error se reduce a la mitad en cada paso.
Si hay más de una raíz en el intervalo inicial, el método de bisección encontrará una de ellas, pero no siempre es fácil saber cuál.
Cota de Error
Después de realizar 'n' pasos (iteraciones) con el método de bisección, podemos saber qué tan cerca estamos de la raíz verdadera. El error máximo que podemos tener se calcula con esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varepsilon := |r-r_n| \le \frac{b-a}{2^{n+1}}
Aquí, r es la raíz verdadera, rn es la raíz que encontramos después de 'n' pasos, b-a es la longitud de tu intervalo inicial, y 2n+1 significa 2 multiplicado por sí mismo 'n+1' veces.
Si quieres que tu error sea menor que un cierto valor (por ejemplo, muy pequeño), puedes calcular cuántos pasos 'n' necesitas hacer usando esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n = \lceil \log_2\left(\frac{b - a}{\varepsilon}\right) \rceil - 1
Esto te dice el número mínimo de iteraciones para alcanzar la precisión deseada.
Galería de imágenes
-
Unas cuantas iteraciones del método de bisección aplicadas en un intervalo [a1;b1]. El punto rojo es la raíz de la función.
Véase también
En inglés: Bisection method Facts for Kids
