Frecuencia modulada para niños

No debe confundirse con Radio FM.

«FM» redirige aquí. Para otras acepciones, véase Fm.

Datos para niños Técnicas de modulación
Modulación analógica
AM FM PM QAM DSB SSB
Modulación digital
ASK APSK CPM FSK GMFK GMSK MFSK MSK OOK PPM PSK QAM SC-FDMA TCM
Espectro disperso
CSS DSSS FHSS THSS
Ver también
Detección y corrección de errores Demodulación Códigos en línea Módem PAM PCM PWM ΔΣM OFDM
v t e

Una señal moduladora (la primera) puede transmitirse modulando una onda portadora en AM (la segunda) o FM (la tercera), entre otras.

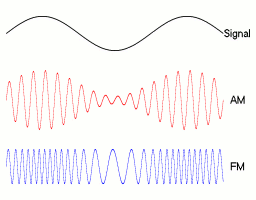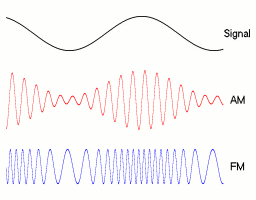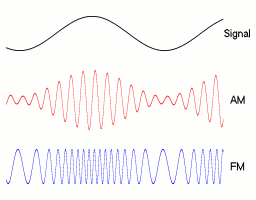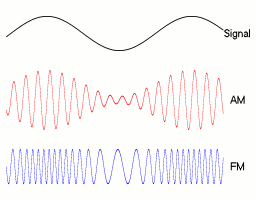
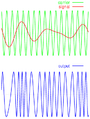
La frecuencia modulada (FM), o modulación de frecuencia, es una técnica de modulación angular que permite transmitir información a través de una onda portadora variando su frecuencia. En aplicaciones analógicas, la frecuencia instantánea de la señal modulada es proporcional al valor instantáneo de la señal moduladora. Se puede enviar datos digitales por el desplazamiento de la onda de frecuencia entre un conjunto de valores discretos, modulación conocida como modulación por desplazamiento de frecuencia.

La modulación de frecuencia se usa comúnmente en la banda de muy alta frecuencia para radiodifusión de la música y el habla y de audio en televisión analógica. Se utiliza una transmisión de banda estrecha o N-FM (de la sigla en inglés "Narrow-FM") para comunicaciones de voz en la radio de dos vías, a diferencia del tipo que se usa en la radiodifusión comercial FM que se llama FM de banda ancha o W-FM. (de la siglas en inglés "Wide-FM"). Además, se utiliza para enviar señales al espacio.

La modulación de frecuencia también se utilizó en las frecuencias intermedias en la mayoría de los sistemas de vídeo analógico, incluyendo el sistema VHS, para registrar la luminancia (señal de blanco y negro) de la señal de video. La modulación de frecuencia es el único método factible para la grabación de video y para reproducir la cinta magnética sin la distorsión extrema, como las señales de vídeo con una gran variedad de componentes de frecuencia, de unos pocos hercios a varios megahercios.

Dentro de los avances más importantes que se presentan en las comunicaciones, uno de los más importantes es, sin duda, la mejora de un sistema de transmisión y recepción en características como la relación señal-ruido, pues permite una mayor seguridad en las mismas. Es así como el paso de modulación de amplitud (AM), a la modulación de frecuencia (FM) establece un importante avance no solo en el mejoramiento que presenta la relación señal ruido, sino también en la mayor resistencia al efecto del desvanecimiento y a la interferencia, tan comunes en AM.

La modulación en frecuencia (FM) tiene un mejor rechazo a la interferencia electromagnética que AM, como se muestra en esta dramática demostración publicitaria en Nueva York realizada por General Electric en 1940. Cerca del prototipo de receptor de radio (en el centro) que contenía receptores para AM y FM se realizó una descarga eléctrica de un millón de voltios. Durante la sintonía en AM, el grado de interferencia fue tal que solo logró escucharse el resultado de la descarga eléctrica. Cuando se cambió al modo FM, la música logró escucharse con sólo una pequeña cantidad de estática.

La modulación de frecuencia también se utiliza en las frecuencias de audio para sintetizar sonido. Esta técnica, conocida como síntesis FM, fue popularizada en los inicios de los sintetizadores digitales y se convirtió en una característica estándar para varias generaciones de tarjetas de sonido de computadoras personales.

Contenido

Terminología
Teoría Matemática
- Fundamentos
- Funciones de Bessel
Regla de Carson
Aplicaciones en radio
Otras aplicaciones
Tecnología
Véase también

Terminología

Esta técnica se denomina «modulación de frecuencia», aunque también se usa el término «frecuencia modulada», del inglés «frequency modulation», sinónimo del primero. Como abreviatura de ambas denominaciones se usa la sigla «FM».

Teoría Matemática

Fundamentos

Una señal senoidal se expresa generalmente como:

(1) $x(t) = A \cos (\phi(t)) = A \, cos (\omega_c t+\theta(t))$

donde:

$A$ : amplitud de la señal.

$\phi(t)$ : fase instantánea de la señal senoidal.

$\omega$ _c: frecuencia angular constante de la señal y

$\theta(t)$ : desviación de fase.

En la modulación angular, la amplitud de una señal senoidal, denominada portadora, se mantiene constante y la desviación de fase cambia continuamente con el tiempo de modo que su frecuencia angular instantánea en determinado momento $t$ es:

(2) $\phi(t) = \frac{d(\omega_c t + \theta(t))}{dt} = \omega_c + \frac{d\theta}{dt}$

Donde $\frac{d\theta}{dt}$ es la desviación de frecuencia instantánea y, por lo tanto, la fase instantánea $\phi(t)$ en todo momento es la integral de la ecuación (2) respecto al tiempo:

(3) $\phi(t) = \omega_c t + \int_0^t \dfrac{d\theta}{dt} dt$

En la modulación de frecuencia, la desviación de frecuencia instantánea es proporcional al valor instantáneo de la señal moduladora $v_m(t)$ . La constante de proporcionalidad, en este caso es $K_1$ . Matemáticamente, esto se expresa así:

(4) $\frac{d\theta}{dt} = K_1 v_m(t)$

Por lo tanto, la ecuación (3) toma la forma:

(5) $\phi(t) = \omega_c t + \int_0^t K_1 v_m(t)$

Incluyendo la igualdad (5) dentro de (1) se obtiene:

(6) $x_c(t) = A_c cos\left(\omega_c t + K_1 \int_0^t v_m(t) dt\right)$

donde $A_c$ es la amplitud de la portadora y $\omega_c$ es su frecuencia angular sin modulación. El factor de proporcionalidad $K_1$ es también conocido como sensibilidad a la desviación del modulador de frecuencia cuya unidad es radianes/(V*s).

Asumiendo que la señal moduladora es senoidal, es decir que $v_m(t) = A_m cos \, \omega_m t$ la expresión para (6) queda como:

(7) $x_c(t) = A_c \cos\left(\omega_c t + \dfrac{K_1 A_m}{\omega_m} sen \, \omega_m t \right)$

La expresión que acompaña en (7) a la función seno es el índice de modulación para FM $m$ :

$m = \dfrac{K_1 A_m}{\omega_m}$

el cual carece de unidad de medida, así que la ecuación (7) se puede reescribir como:

(8) $y(t) = A_c \cos\left(\omega_c t + m sen \, \omega_m t \right)$

Funciones de Bessel

En el caso anterior, en el cual la portadora es modulada por una onda senoidal, el espectro de frecuencia resultante no se puede expresar de manera sencilla con la transformada de Fourier, pero se puede calcular utilizando las funciones de Bessel de primera especie de orden n-ésimo $J_n(m)$ , en función del número de bandas laterales y el índice de modulación m. Las amplitudes de portadora y las bandas laterales se ilustran para diferentes índices de modulación de señales FM y en los casos en que esta cifra no es visible, se debe a que la amplitud de tales bandas es menor a 0,01. Para ciertos valores particulares del índice de modulación, la amplitud de la portadora se convierte en cero y toda la potencia de la señal está en las bandas laterales. Como ejemplo, una desviación de 3 kHz provocada por una senoidal modulante de 2 kHz, resulta en un índice de modulación de 1,5, del cual salen 8 bandas laterales, a ambos lados de la señal portadora. La tabla adjunta muestra algunos valores de $J_n(m)$ respecto a $m$ , teniendo en cuenta que solo se visualiza la mitad de las bandas laterales, ya que las demás son iguales en amplitud:

Índice de Modulación	Amplitud de las bandas laterales $J_n(m)$
Índice de Modulación	Portadora	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
0.00	1.00
0.25	0.98	0.12
0.5	0.94	0.24	0.03
1.0	0.77	0.44	0.11	0.02
1.5	0.51	0.56	0.23	0.06	0.01
2.0	0.22	0.58	0.35	0.13	0.03
2.41	0.00	0.52	0.43	0.20	0.06	0.02
2.5	−0.05	0.50	0.45	0.22	0.07	0.02	0.01
3.0	−0.26	0.34	0.49	0.31	0.13	0.04	0.01
4.0	−0.40	−0.07	0.36	0.43	0.28	0.13	0.05	0.02
5.0	−0.18	−0.33	0.05	0.36	0.39	0.26	0.13	0.05	0.02
5.53	0.00	−0.34	−0.13	0.25	0.40	0.32	0.19	0.09	0.03	0.01
6.0	0.15	−0.28	−0.24	0.11	0.36	0.36	0.25	0.13	0.06	0.02
7.0	0.30	0.00	−0.30	−0.17	0.16	0.35	0.34	0.23	0.13	0.06	0.02
8.0	0.17	0.23	−0.11	−0.29	−0.10	0.19	0.34	0.32	0.22	0.13	0.06	0.03
8.65	0.00	0.27	0.06	−0.24	−0.23	0.03	0.26	0.34	0.28	0.18	0.10	0.05	0.02
9.0	−0.09	0.25	0.14	−0.18	−0.27	−0.06	0.20	0.33	0.31	0.21	0.12	0.06	0.03	0.01
10.0	−0.25	0.04	0.25	0.06	−0.22	−0.23	−0.01	0.22	0.32	0.29	0.21	0.12	0.06	0.03	0.01
12.0	0.05	−0.22	−0.08	0.20	0.18	−0.07	−0.24	−0.17	0.05	0.23	0.30	0.27	0.20	0.12	0.07	0.03	0.01

Regla de Carson

Artículo principal: Regla de Carson

En una ponencia de 1922, el ingeniero e inventor estadounidense John Renshaw Carson desarrolló una regla general que establece que casi toda la potencia (aproximadamente, el 98 %) de una señal modulada en frecuencia, se encuentra dentro de un ancho de banda $B_T$ de:

$B_T = 2 (\Delta f + f_m) = 2 f_m (m+1)$

donde $\Delta f$ es la desviación de frecuencia y $f_m = \dfrac{\omega_c}{2 \pi}$ es la máxima frecuencia de modulación. La condición para que se aplique dicha regla es que la señal moduladora sea senoidal. En caso de no ser así, se aplica una ecuación semejante a la anterior:

$B_T = 2 (\Delta f + W) = 2 W (D+1)$

Una vez más, $\Delta f$ es la desviación de frecuencia, $W$ es la máxima frecuencia de la señal moduladora y $D$ es la relación de desviación, que es la relación entre la desviación de frecuencia y la frecuencia más alta de la señal de modulación no sinusoidal.

Aplicaciones en radio

Un ejemplo de modulación de frecuencia. El diagrama superior muestra la señal moduladora superpuesta a la onda portadora. El diagrama inferior muestra la señal modulada resultante.

El ingeniero e inventor estadounidense Edwin Armstrong presentó su estudio Un método de reducción de molestias en la radio mediante un sistema de modulación por frecuencia, que describió por primera vez la FM, antes que la sección neoyorquina del Instituto de Ingenieros de Radio el 6 de noviembre de 1935. El estudio fue publicado en 1935.

La FM para radiodifusión de banda ancha (W-FM) requiere un mayor ancho de banda que la modulación de amplitud para la misma señal moduladora, pero a su vez hace a la señal más resistente al ruido y la interferencia. La modulación de frecuencia es también más resistente al fenómeno del desvanecimiento, muy común en la AM. Por estas razones, la FM fue escogida como el estándar para la transmisión de radio de alta fidelidad, resultando en el término "Radio FM" (aunque por muchos años la BBC la llamó "Radio VHF", ya que la radiodifusión en FM usa una parte importante de la banda VHF).

Los receptores de radio FM emplean un detector adecuado para señales FM y exhiben un fenómeno llamado efecto de captura, en el cual el sintonizador es capaz de recibir la señal más fuerte de las que transmitan en la misma frecuencia. Sin embargo, la desviación por frecuencia o falta de selectividad puede causar que una estación o señal sea repentinamente tomada por otra en un canal adyacente. La desviación por frecuencia generalmente constituyó un problema en receptores viejos o baratos, mientras que la selectividad inadecuada puede afectar a cualquier aparato.

Una señal FM también puede usarse para transportar una señal estereofónica. No obstante, esto se hace mediante el uso de multiplexación y demultiplexación antes y después del proceso de la FM: Se compone una señal moduladora (en banda base) con la suma de los dos canales (izquierdo y derecho), y se añade un tono piloto a 19 kHz; se modula a continuación una señal diferencia de ambos canales a 38 kHz en doble banda lateral y se le añade a la moduladora anterior. De este modo se consigue compatibilidad con receptores antiguos que no sean estereofónicos, y además la implementación del demodulador es muy sencilla.

Se puede usar una amplificación de conmutación de frecuencias radiales de alta eficiencia para transmitir señales FM (y otras señales de amplitud constante). Para una intensidad de señal dada (medida en la antena del receptor), los amplificadores de conmutación utilizan menos potencia y cuestan menos que un amplificador lineal. Esto le da a la FM otra ventaja sobre otros esquemas de modulación que requieren amplificadores lineales, como la AM y la QAM.

Otras aplicaciones

La modulación de frecuencia encuentra aplicación en gran cantidad de sistemas de comunicación. La separación entre dos canales adyacentes es de 200 kHz y la desviación por frecuencia $\Delta f=\pm75\, kHz$ . Aparte de la FM de radiodifusión, entre 87 y 108 MHz, la modulación de frecuencia se usa también en las siguientes aplicaciones:

Televisión:
- Subportadora de sonido: La información de sonido modula en frecuencia la subportadora de sonido, que posteriormente se une a las restantes componentes de la señal de TV para modular en AM la portadora del canal correspondiente y se filtra para obtener la banda lateral vestigial. El sonido NICAM es digital y no sigue este proceso.
- Sistema de color SECAM: En el sistema de televisión analógica en color SECAM se modula la información de color en FM.
Micrófonos inalámbricos: Debido a la mayor robustez de esta técnica ante las interferencias (ruidos radioeléctricos externos).
Ayudas a la navegación aérea: Sistemas como el DVOR (VOR Doppler) simulan una antena giratoria que, por efecto Doppler, modula en frecuencia la señal transmitida.

Tecnología

Modulador de FM

Tramsmisor FM de una radiodifusora.

La modulación de una portadora sobre FM, aunque se puede realizar de varias formas, resulta un problema delicado debido a que se necesitan dos características contrapuestas: estabilidad de frecuencia y que la señal moduladora varíe la frecuencia. Por ello, la solución simple de aplicar la señal moduladora, de manera directa, a un oscilador controlado por tensión (VCO) no es satisfactoria.

Modulación del oscilador. En un oscilador estable, controlado con un cristal piezoeléctrico, se añade un condensador variable con la señal moduladora (varactor). Eso varía ligeramente la frecuencia del oscilador en función de la señal moduladora. Como la excursión de frecuencia que se consigue no suele ser suficiente, se lleva la señal de salida del oscilador a multiplicadores de frecuencia para alcanzar la frecuencia de radiodifusión y desviación de frecuencia necesaria.
Moduladores de fase. Un modulador de FM se puede modelar exactamente como un modulador de PM con un integrador a la entrada de la señal moduladora.
Modulador con Bucle de enganche de fase (PLL). En este caso se incorpora el VCO, pero ahora su salida se compara con una frecuencia de referencia para obtener una señal de error, de modo que se tiene una realimentación negativa que minimiza dicho error. La señal de error se filtra para que sea insensible a las variaciones dentro del ancho de banda de la señal moduladora, puesto que estas variaciones son las que modulan la salida del VCO. Este método se ha impuesto con la llegada de los PLL integrados ya que ha pasado de ser el método más complejo y costoso a ser uno muy económico. Presenta otras ventajas, como el poder cambiar de frecuencia para pasar de un canal a otro y mantener coherentes todas las frecuencias del sistema...

Demodulador de FM

Como en el caso del modulador, también es más complejo que el de AM. Se utilizan sobre todo dos métodos:

Discriminador reactivo. Se basa en llevar la señal de FM a una reactancia, normalmente bobinas acopladas, de forma que su impedancia varíe con la frecuencia. La señal de salida aparece, entonces, modulada en amplitud y se detecta con un detector de envolvente. Hasta la llegada de dispositivos semiconductores, existían válvulas específicas para esta tarea, consistentes en un doble-diodo-triodo. Los dos diodos forman el detector de envolvente y el triodo amplifica la señal, mejorando la relación señal/ruido.
Detector con PLL. La señal del PLL proporciona la señal demodulada. Existen muchas variaciones según la aplicación, pero estos detectores suelen estar en circuitos integrados que, además, contienen los amplificadores de RF y de frecuencia intermedia. Existen circuitos integrados que realmente son una radio de FM monofónica completa, como el dispositivo TDA7000.

Consideración del ancho de banda

Al contrario que en el caso de modulación de amplitud, que se concentra en la frecuencia portadora y dos bandas laterales, el ancho de banda de una señal de FM se extiende indefinidamente teniendo como una amplitud estándar o de rango de transferencia de 58 kHz con 6 canales de transferencia, cancelándose solamente en ciertos valores de frecuencia discretos. Cuando la señal moduladora es senoidal, el espectro de potencia resultante es discreto y simétrico respecto de la frecuencia de la portadora, y la contribución de cada frecuencia al espectro de la señal modulada tiene que ver con las funciones de Bessel de primera especie, como se indicó anteriormente.

Véase también

En inglés: Frequency modulation Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Frecuencia_modulada&oldid=3849592»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Frecuencia modulada para Niños. Enciclopedia Kiddle.