Mediana (estadística) para niños
La mediana es un concepto importante en estadística. Imagina que tienes una lista de números y los ordenas de menor a mayor. La mediana es el número que se encuentra justo en el medio de esa lista. Es como encontrar el punto central de tus datos.
Si tienes una cantidad impar de números, la mediana es el número que está exactamente en el centro. Por ejemplo, si tienes 5 números, la mediana es el tercer número una vez que los has ordenado.
Si tienes una cantidad par de números, no hay un solo número en el centro. En este caso, la mediana se calcula tomando los dos números del medio, sumándolos y dividiendo el resultado entre dos. Es decir, es el promedio de esos dos números centrales.
Contenido
¿Qué es la Mediana en Estadística?
La mediana es el valor que divide un conjunto de datos ordenados en dos mitades iguales. La mitad de los datos son menores o iguales que la mediana, y la otra mitad son mayores o iguales. Es una forma de encontrar el "valor típico" o central de un grupo de números.
Cómo Calcular la Mediana en Conjuntos de Números
Para encontrar la mediana, el primer paso siempre es ordenar los números de menor a mayor.
Mediana con un Número Impar de Datos
Cuando tienes una cantidad impar de números en tu lista, la mediana es el número que está justo en el centro.
- Ejemplo: Si tienes los números 1, 3, 3, 6, 7, 8, 9.
* Hay 7 números en total (una cantidad impar). * El número que está en la posición central es el 6. * Por lo tanto, la mediana es 6.
Mediana con un Número Par de Datos
Cuando tienes una cantidad par de números en tu lista, no hay un solo número en el centro. En este caso, la mediana es el promedio de los dos números que se encuentran en las posiciones centrales.
- Ejemplo: Si tienes los números 1, 2, 3, 4, 5, 6, 8, 9.
* Hay 8 números en total (una cantidad par). * Los dos números centrales son el 4 y el 5. * Para encontrar la mediana, sumamos 4 + 5 = 9 y dividimos entre 2. * La mediana es 4.5.
¿Por qué es útil la Mediana?
La mediana es muy útil porque no se ve afectada por valores extremos. Esto significa que si hay algunos números muy grandes o muy pequeños en tu lista, la mediana sigue siendo un buen representante del "centro" de tus datos.
- Ejemplo: Imagina que quieres saber cuánto tiempo tardan los estudiantes en terminar una carrera. Si algunos estudiantes tardan muchos años (por ejemplo, porque trabajan al mismo tiempo), estos valores muy altos podrían hacer que el promedio (la media) parezca más alto de lo que realmente es para la mayoría. La mediana, en cambio, te daría un valor más representativo del tiempo que tarda la mayoría de los estudiantes, porque esos valores extremos no la "jalan" tanto.
La mediana es fácil de entender y calcular, lo que la convierte en una herramienta popular en estadística descriptiva para resumir datos.
Comparación con otras Medidas Centrales
Para entender mejor la mediana, podemos compararla con otras formas de encontrar el "centro" o características de un conjunto de datos.
| Tipo | Descripción | Ejemplo | Resultado |
|---|---|---|---|
| Rango medio | El punto medio entre el número más pequeño y el más grande de un conjunto de datos. | 1, 2, 2, 3, 4, 7, 9 | 5 |
| Media aritmética | La suma de todos los valores de un conjunto de datos dividida por la cantidad de valores. También se le llama promedio. | (1 + 2 + 2 + 3 + 4 + 7 + 9) / 7 | 4 |
| Mediana | El valor intermedio que separa la mitad de los valores mayores y la mitad de los valores menores de un conjunto de datos. | 1, 2, 2, 3, 4, 7, 9 | 3 |
| Rango | La diferencia entre el valor más grande y el valor más pequeño. | 1, 2, 2, 3, 4, 7, 9 | 8 |
| Moda | El valor que aparece con mayor frecuencia en un conjunto de datos. | 1, 2, 2, 3, 4, 7, 9 | 2 |
Cálculo de la Mediana para Datos Agrupados
A veces, los datos se presentan en tablas donde los números están agrupados en categorías o intervalos. Calcular la mediana en estos casos es un poco diferente, pero sigue la misma idea de encontrar el punto medio.
Ejemplo 1: Cantidad Impar de Datos Agrupados
Imagina que tenemos las calificaciones de 39 alumnos en Matemáticas, organizadas en una tabla:
| Calificaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Número de alumnos | 2 | 2 | 4 | 5 | 8 | 9 | 3 | 4 | 2 |
| Frecuencia absoluta acumulada | 2 | 4 | 8 | 13 | 21 | 30 | 33 | 37 | 39 |
Como hay 39 alumnos (un número impar), la posición de la mediana es (39 + 1) / 2 = 20. Buscamos la calificación que ocupa la posición 20. Mirando la fila de "Frecuencia absoluta acumulada":
- Hasta la calificación 4, hay 13 alumnos.
- Hasta la calificación 5, hay 21 alumnos.
Esto significa que el alumno número 20 está en la categoría de calificación 5. Por lo tanto, la mediana es 5 puntos. Esto nos dice que la mitad de la clase obtuvo un 5 o menos, y la otra mitad obtuvo un 5 o más.
Ejemplo 2: Cantidad Par de Datos Agrupados
Ahora, veamos un ejemplo con 38 alumnos:
| Calificaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Número de alumnos | 2 | 2 | 4 | 5 | 6 | 9 | 4 | 4 | 2 |
| Frecuencia absoluta acumulada | 2 | 4 | 8 | 13 | 19 | 28 | 32 | 36 | 38 |
Como hay 38 alumnos (un número par), necesitamos encontrar los dos valores centrales. Las posiciones centrales son 38 / 2 = 19 y (38 / 2) + 1 = 20. Mirando la fila de "Frecuencia absoluta acumulada":
- Hasta la calificación 5, hay 19 alumnos.
- Hasta la calificación 6, hay 28 alumnos.
Esto significa que el alumno en la posición 19 tiene una calificación de 5, y el alumno en la posición 20 tiene una calificación de 6. Para encontrar la mediana, promediamos estos dos valores: (5 + 6) / 2 = 5.5. Así, la mediana es 5.5 puntos. Esto significa que la mitad de la clase obtuvo un 5.5 o menos, y la otra mitad un 5.5 o más.
Galería de imágenes
-
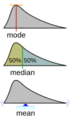
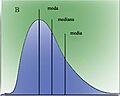
Visualización geométrica de la moda, la mediana y de la media de una función arbitraria de densidad de probabilidad.
Véase también
 En inglés: Median Facts for Kids
En inglés: Median Facts for Kids