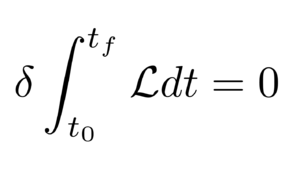Mecánica hamiltoniana para niños
La mecánica hamiltoniana es una forma especial de entender cómo se mueven las cosas en el universo, como los planetas o una pelota que lanzas. Fue creada en 1833 por un científico llamado William Rowan Hamilton. Es como una versión diferente de la mecánica clásica, que es la forma más conocida de describir el movimiento, como las leyes de Newton.
La mecánica hamiltoniana es muy útil porque, aunque describe lo mismo, lo hace de una manera que a veces es más sencilla de resolver o que ayuda a entender mejor algunos conceptos avanzados de la física.
¿Qué es la Mecánica Hamiltoniana?
¿Cómo se relaciona con la mecánica lagrangiana?
En la mecánica lagrangiana, otra forma de describir el movimiento, las ecuaciones que nos dicen cómo se mueven las cosas son un poco complicadas. Son ecuaciones de "segundo orden", lo que significa que involucran cambios de velocidad (aceleración). Para resolverlas, necesitamos saber la posición y la velocidad de un objeto en un momento dado.
La mecánica hamiltoniana es muy parecida, pero usa un truco para que las ecuaciones sean más fáciles. En lugar de usar las "velocidades generalizadas" (que son como las velocidades normales pero adaptadas a diferentes sistemas de coordenadas), introduce algo llamado "momentos conjugados". Estos momentos son como una versión especial del momento lineal (masa por velocidad).
Así, por cada velocidad, hay un momento conjugado. Si el sistema es sencillo, este momento conjugado es el mismo que el momento que ya conoces. Por ejemplo, si usas coordenadas polares, el momento conjugado de la velocidad angular es el momento angular.
El corazón de la mecánica hamiltoniana es una función especial llamada hamiltoniano, que se representa con la letra H. En muchos casos, este hamiltoniano representa la energía total del sistema, es decir, la suma de la energía cinética (energía de movimiento) y la energía potencial (energía almacenada).
Ecuaciones de Hamilton: El corazón del movimiento
Una vez que tenemos el hamiltoniano, podemos usarlo para encontrar las "ecuaciones canónicas de Hamilton". Estas ecuaciones son un conjunto de ecuaciones de "primer orden", lo que significa que solo involucran la velocidad, no la aceleración. Esto las hace más fáciles de resolver que las ecuaciones de la mecánica lagrangiana.
Las ecuaciones de Hamilton nos dicen cómo cambian las posiciones y los momentos conjugados de un sistema a lo largo del tiempo. Son como una receta para predecir el futuro de un objeto en movimiento.
(2)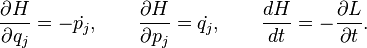
¿Por qué es útil la mecánica hamiltoniana?
Aunque a veces resolver un problema con la mecánica hamiltoniana puede parecer similar a usar la mecánica lagrangiana o las leyes de Newton, tiene varias ventajas importantes:
- Ecuaciones más sencillas: Como las ecuaciones de Hamilton son de primer orden, son más fáciles de manejar matemáticamente.
- Visión más profunda: La mecánica hamiltoniana nos permite entender mejor el "espacio fásico" de un sistema. Imagina que cada punto en este espacio representa una posible combinación de posición y momento de un objeto. La mecánica hamiltoniana nos ayuda a ver cómo se mueve el objeto a través de este espacio.
- Transformaciones especiales: Permite hacer cambios de coordenadas muy útiles, llamadas "transformaciones canónicas". Estas transformaciones pueden simplificar mucho las ecuaciones del movimiento, haciendo que sea más fácil encontrar la solución.
- Simetrías y conservación: Es más fácil identificar qué propiedades de un sistema se mantienen constantes (se "conservan") a lo largo del tiempo. Por ejemplo, si un sistema tiene una simetría, la mecánica hamiltoniana nos ayuda a ver que hay una cantidad que se conserva, como la energía o el momento.
El corchete de Poisson
El corchete de Poisson es una herramienta matemática especial que se usa en la mecánica hamiltoniana. Nos ayuda a entender cómo cambian las propiedades de un sistema con el tiempo. Si el corchete de Poisson de una propiedad con el hamiltoniano es cero, significa que esa propiedad se conserva.
(4)![[F,G]=\sum_i\left[
\frac{\partial F}{\partial q_{i}}\frac{\partial G}{\partial p_{i}} - \frac{\partial F}{\partial p_{i}} \frac{\partial G}{\partial q_{i}}
\right]](/images/math/f/6/6/f66b17f3b78462e17413316af173ee9a.png)
Transformaciones canónicas
Las transformaciones canónicas son como "cambios de gafas" para ver el sistema. Son cambios en las coordenadas (posiciones y momentos) que no alteran la forma de las ecuaciones de Hamilton. Esto es muy útil porque a veces, al cambiar las coordenadas, las ecuaciones se vuelven mucho más simples de resolver.
Teorema de Liouville
El teorema de Liouville es un concepto interesante. Imagina un grupo de puntos en el espacio fásico que representan diferentes estados posibles de un sistema. A medida que estos puntos se mueven con el tiempo, la forma de la región que ocupan puede cambiar, pero el "volumen" total de esa región en el espacio fásico siempre se mantiene igual. Es como si el espacio fásico fuera un fluido incompresible.
Mecánica hamiltoniana avanzada
La mecánica hamiltoniana también se puede describir con matemáticas más complejas, usando algo llamado "geometría diferencial". Esto permite a los científicos estudiar el movimiento de una manera muy abstracta y elegante, lo que es fundamental para entender teorías más avanzadas de la física.
En esta forma avanzada, el sistema se describe con una "variedad simpléctica", que es un espacio matemático especial. El hamiltoniano se convierte en una función en este espacio, y las ecuaciones de Hamilton se expresan de una manera muy compacta y poderosa.
Flujo hamiltoniano
El hamiltoniano también define un "flujo" en el espacio fásico. Imagina que cada punto en este espacio sigue un camino, como si fuera una corriente de agua. Estos caminos son las trayectorias que siguen los sistemas físicos. El teorema de Liouville, por ejemplo, nos dice que este flujo no "comprime" ni "expande" el volumen en el espacio fásico.
Véase también
 En inglés: Hamiltonian mechanics Facts for Kids
En inglés: Hamiltonian mechanics Facts for Kids
- Mecánica lagrangiana
- Mecánica routhiana