Magnitud aparente para niños
La magnitud aparente es una forma de medir qué tan brillante se ve una estrella o cualquier otro objeto en el espacio desde la Tierra. Imagina que tienes una linterna muy potente: si está cerca de ti, se verá muy brillante, pero si la alejas mucho, parecerá más débil. Lo mismo ocurre con las estrellas.
La magnitud aparente depende de tres cosas principales:
- Qué tan brillante es el objeto en realidad (su luminosidad).
- Qué tan lejos está de nosotros.
- Si hay polvo cósmico o gas en el espacio entre nosotros y el objeto, que pueda bloquear parte de su luz.
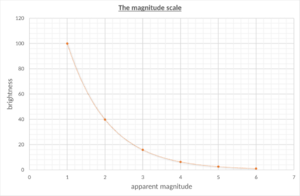
En la antigüedad, hace mucho tiempo, en el siglo II a. C., los astrónomos ya clasificaban las estrellas por su brillo. Las dividían en seis grupos. Las estrellas más brillantes estaban en el grupo 1, y las más débiles que apenas se podían ver a simple vista estaban en el grupo 6. Esta forma de clasificar se basaba en cómo el ojo humano percibe la luz, que no es de forma lineal. Esto significa que si una estrella es 10 veces más brillante que otra, nuestros ojos no la perciben como 10 veces más brillante, sino de una manera diferente. Por eso, la escala de brillo es logarítmica.
Hoy en día, la escala de magnitud aparente puede tener valores negativos y positivos. Cuanto más bajo es el número (o más negativo), más brillante es el objeto. Por ejemplo, el Sol es el objeto más brillante que vemos, y su magnitud aparente es de -26.7. En cambio, el telescopio espacial Hubble puede ver objetos muy, muy débiles, con magnitudes aparentes de hasta +31.5.
Para medir la magnitud aparente de un objeto, los científicos usan una técnica llamada fotometría. Esto implica usar instrumentos especiales con filtros que solo dejan pasar ciertos colores de luz. Dependiendo de cómo se mida, hay diferentes sistemas de magnitud.
Si medimos el brillo solo en la parte del espectro luminoso que podemos ver con nuestros ojos, se llama magnitud visual. Si medimos toda la luz que emite un objeto, incluyendo la que no podemos ver (como la infrarroja o ultravioleta), se llama magnitud bolométrica.
Para que todos los astrónomos puedan comparar sus mediciones, se necesita un punto de referencia. La estrella Vega se usa a menudo como ese punto de referencia, asignándole una magnitud de cero.
Contenido
¿Cómo se descubrió la escala de brillo de las estrellas?
La idea de clasificar las estrellas por su brillo viene de la antigua Grecia. Los astrónomos de esa época dividieron las estrellas visibles a simple vista en seis grupos. Las más brillantes eran de "primera magnitud" y las más débiles eran de "sexta magnitud". Se cree que esta idea pudo haberla tenido Hiparco de Nicea y fue popularizada por Claudio Ptolomeo en su libro Almagesto. En ese tiempo, pensaban que una estrella de una magnitud era el doble de brillante que una de la siguiente magnitud.
En 1856, un astrónomo llamado Norman Pogson mejoró este sistema. Él se dio cuenta de que una estrella de primera magnitud es en realidad 100 veces más brillante que una de sexta magnitud. Esto significa que la diferencia de brillo entre una magnitud y la siguiente no es el doble, sino un factor de aproximadamente 2.512. A este número se le conoce como el "cociente de Pogson".
Al principio, la estrella Polaris se usaba como referencia para la magnitud 2. Pero como Polaris cambia un poco de brillo, ahora se usa la estrella Vega como el punto cero de la magnitud aparente para la mayoría de las mediciones.
| Apertura del telescopio (mm) |
Magnitud más débil que se puede ver |
|---|---|
| 35 | 11.3 |
| 60 | 12.3 |
| 102 | 13.3 |
| 152 | 14.1 |
| 203 | 14.7 |
| 305 | 15.4 |
| 406 | 15.7 |
| 508 | 16.4 |
Con los sistemas modernos, las magnitudes aparentes pueden ser números negativos para objetos muy brillantes. Por ejemplo, Sirio, la estrella más brillante en nuestro cielo nocturno, tiene una magnitud de -1.4. Otros objetos muy brillantes como Venus, Marte y Júpiter también tienen magnitudes negativas.
¿Cómo se calcula la magnitud aparente?
La magnitud aparente se calcula usando una fórmula matemática que tiene logaritmos. No te preocupes por los detalles de la fórmula, lo importante es entender que:
- Una diferencia de 5 magnitudes significa que un objeto es 100 veces más brillante que otro.
- Cada aumento de una magnitud significa que el brillo disminuye en un factor de 2.512 (el cociente de Pogson).
Esto nos permite comparar el brillo de dos objetos celestes.
Sistemas de magnitud
Además del sistema que usa Vega como referencia (llamado VegaMAG), existen otros sistemas para definir el punto cero de la magnitud aparente, como ABMAG y STMAG. Estos sistemas se basan en cómo se distribuye la energía de la luz de una estrella.
Otras formas de medir el brillo
Magnitud absoluta
La magnitud aparente nos dice qué tan brillante se ve una estrella desde la Tierra. Pero, ¿qué tan brillante es en realidad? Para saberlo, los astrónomos usan la magnitud absoluta. Esta es la magnitud que tendría una estrella si estuviera a una distancia estándar de 10 pársecs (aproximadamente 32.6 años luz) de nosotros.
La magnitud absoluta nos ayuda a comparar el brillo real de las estrellas, sin importar qué tan lejos estén. También se hacen ajustes si hay polvo en el espacio que bloquea la luz.
Magnitud bolométrica
La magnitud bolométrica es una medida del brillo total de una estrella en todas las longitudes de onda de luz que emite, no solo la que podemos ver. Es como medir toda la energía que irradia una estrella. Para calcular la magnitud bolométrica absoluta de una estrella, se compara su luminosidad (su brillo real) con la del Sol.
Ejemplos de brillo
Para entender mejor, comparemos el brillo del Sol y la Luna llena:
- La magnitud aparente del Sol es de -26.832 (muy brillante).
- La magnitud aparente de la Luna llena es de -12.74 (mucho más débil que el Sol).
Si calculamos la diferencia de brillo, el Sol parece unas 432,513 veces más brillante que la Luna llena. ¡Es una diferencia enorme!
¿Cómo se mide con precisión?
Para medir la magnitud aparente con mucha precisión, los astrónomos usan telescopios y cámaras especiales. Necesitan calibrar sus equipos, lo que significa compararlos con estrellas cuyo brillo ya se conoce muy bien. También deben tener en cuenta cómo la atmósfera terrestre afecta la luz de las estrellas, ya que el aire puede absorber o dispersar parte de la luz.
Los astrónomos observan varias estrellas de referencia y ajustan sus mediciones para saber el brillo real que tendrían los objetos si no hubiera atmósfera. Esto es importante para que los datos de diferentes observatorios puedan compararse correctamente.
Véase también
 En inglés: Magnitude (astronomy) Facts for Kids
En inglés: Magnitude (astronomy) Facts for Kids