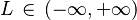Joseph Ludwig Raabe para niños
Datos para niños Joseph Ludwig Raabe |
||
|---|---|---|
 |
||
| Información personal | ||
| Nacimiento | 15 de mayo de 1801 Brody, |
|
| Fallecimiento | 22 de enero de 1859 Zürich, |
|
| Educación | ||
| Educado en | Universidad Técnica de Viena (1821-1827) | |
| Alumno de | Joseph Johann Littrow | |
| Información profesional | ||
| Área | Matemáticas | |
| Conocido por | Criterio de convergencia de Raabe | |
| Empleador |
|
|
| Obras notables | Criterio de Raabe | |
Joseph Ludwig Raabe, también conocido como Josef Rabe, fue un importante profesor y matemático suizo del siglo XIX. Nació el 15 de mayo de 1801 en Brody, Galitzia, y falleció el 22 de enero de 1859 en Zúrich, Suiza.
Es famoso por haber creado el Criterio de Raabe, una herramienta matemática que ayuda a saber si una serie infinita de números se acerca a un valor fijo (converge) o si crece sin límite (diverge). También hizo aportes importantes relacionados con la función gamma. Publicó varios trabajos, como Die Jacob Bernoullische Function (La función Jacobi-Bernoulliana) en 1848.
Contenido
Joseph Ludwig Raabe: Un Matemático Brillante
¿Quién fue Joseph Ludwig Raabe?
Joseph Ludwig Raabe fue un matemático muy dedicado. A pesar de tener un comienzo de vida difícil, logró convertirse en un profesor respetado. Su trabajo más conocido es el Criterio de Raabe, que es una regla para entender el comportamiento de las series matemáticas.
Los Primeros Años de Raabe
La infancia de Joseph Raabe fue complicada. Sus padres tenían una situación económica difícil, lo que hizo que no pudiera ir a una escuela de buena calidad como otros niños de su época.
Su Camino hacia la Educación
A pesar de las dificultades, Joseph estaba muy interesado en las matemáticas. Decidió aprender por su cuenta. Incluso empezó a dar clases particulares a otros estudiantes para ganar dinero y seguir aprendiendo. Mientras enseñaba, también dedicaba tiempo a estudiar nuevos conceptos.
Sus Estudios y Primeros Trabajos
Cuando cumplió 19 años, Raabe había ahorrado suficiente dinero gracias a sus clases. Esto le permitió viajar a Viena para estudiar en el Colegio Politécnico de Austria. Allí, pudo mejorar sus conocimientos en matemáticas.
Un Nuevo Comienzo en Viena
En Viena, Joseph siguió dando clases para pagar sus estudios. Fue en esta ciudad donde conoció y se hizo amigo del astrónomo Joseph Johann von Littrow. Littrow lo animó a publicar sus primeros trabajos en una importante revista de matemáticas llamada Journal für die reine und angewandte Mathematik.
Sus primeros escritos aparecieron en esta revista en 1826 y 1827. Al principio, firmaba como "L. Rabe", pero luego empezó a usar "Joseph L. Raabe". En 1831, debido a una enfermedad que se extendió por Europa, Raabe decidió mudarse. Un amigo lo convenció de ir a Zúrich, Suiza, donde finalmente se graduó en 1833.
El Famoso Criterio de Raabe
Un año después de graduarse, Raabe presentó el criterio matemático por el que se hizo famoso. Este criterio es una extensión de una regla anterior, el Criterio del cociente, creado por Jean le Rond d'Alembert.
¿Qué es el Criterio de Convergencia?
El Criterio de Raabe es una herramienta para saber si una serie infinita (una suma de muchos números que siguen un patrón) converge o diverge. En palabras sencillas, ayuda a determinar si la suma de esos números se acerca a un valor específico o si crece sin parar.
El Criterio de Raabe dice que si tienes una serie de números positivos y calculas un límite especial, puedes saber si la serie converge (si el límite es mayor que 1) o diverge (si el límite es menor que 1).
""Sea una serie, tal que
(serie de términos positivos). Si existe el límite
entonces, si
, siendo
la serie es convergente y si
la serie es divergente."
Joseph Ludwig Raabe.
La primera vez que se publicó el Criterio de Raabe fue en el volumen 11 de la revista de Crelle, con el título Theorie der zur Convergenz und der Divergenz Reihen (Teoría de la convergencia y divergencia de series).
Su Carrera como Profesor y Publicaciones Importantes
En 1836, Joseph Raabe fue nombrado profesor de matemáticas en la Universidad de Zúrich. Aunque no era un puesto fijo al principio, siguió investigando. Trabajó junto a su colega Karl Heinrich Gräffe y ambos hicieron importantes contribuciones a las matemáticas, incluyendo el trabajo de Raabe sobre los polinomios de Bernoulli.
Obras Destacadas de Raabe
Entre 1848 y 1851, Raabe publicó dos trabajos importantes:
- Die Jacob Bernoullische Function (La función Jacobi-Bernoulliana), un documento de 52 páginas.
- Züruckrechnung Einig Summen und auf die bestimmten Integrale Jakob Bernoullische Function (Recálculo de sumas en integrales definidas por la Función Jacobi-Bernoulliana), un documento más corto.
También publicó tres volúmenes de Differential-und Integralrechnung (Cálculo diferencial e integral) entre 1839 y 1847, y dos volúmenes de Mathematischer Mittheilungen (Sistemas matemáticos de operaciones múltiples) en 1847 y 1848. En 1853, presentó un trabajo titulado Fue der ist Gegenstand der Mathematik? (¿Cuál es el propósito de las matemáticas?).
Los Últimos Años de su Vida
En 1855, se creó la Eidgenössische Polytechnische Schule (Escuela Politécnica Federal de Suiza). Raabe fue nombrado profesor titular de matemáticas en esta nueva institución. Sin embargo, no pudo ejercer el cargo por mucho tiempo. En 1858, decidió retirarse debido a una enfermedad. Falleció en enero de 1859, a los 57 años.
Publicaciones
- Uber Reihen, deren wiederkehren Differenzenreihen (Sobre Series y Rediferenciado de Series) - 1829.
- Differential-und Integralrechnung (Cálculo diferencial e integral), 3 volúmenes - 1839-1847.
- Mathematischer Mittheilungen (Sistemas matemáticos de operaciones múltiples), 2 volúmenes - 1847-1848.
- Die Jacob Bernoullische Function (La función Jacobi-Bernoulliana) - 1848.
- Züruckrechnung Einig Summen und auf die bestimmten Integrale Jakob Bernoullische Function (Recálculo de sumas en integrales definidas por la Función Jacobi-Bernoulliana) - 1851.
- Fue der ist Gegenstand der Mathematik? (¿Cuál es el propósito de las matemáticas?) - 1853.
Véase también
 En inglés: Joseph Ludwig Raabe Facts for Kids
En inglés: Joseph Ludwig Raabe Facts for Kids