Intervalo de predicción para niños
Un intervalo de predicción es una herramienta en estadística que nos ayuda a estimar un rango de valores donde es muy probable que caiga una observación futura. Imagina que tienes los resultados de varios exámenes y quieres predecir qué calificación obtendrás en el próximo. Un intervalo de predicción te daría un rango, por ejemplo, entre 80 y 90, donde tu próxima calificación probablemente estará.
Estos intervalos se usan mucho en el análisis de la regresión, que es una forma de entender cómo se relacionan diferentes datos.
Los intervalos de predicción son diferentes de los intervalos de confianza. Mientras que un intervalo de predicción busca estimar dónde caerá un *evento futuro individual*, un intervalo de confianza busca estimar el valor de una característica de un grupo grande (como el promedio real de una población), que no podemos observar directamente.
Contenido
¿Cómo funcionan los intervalos de predicción?
Por ejemplo, si sabemos que las calificaciones de un examen suelen seguir un patrón específico (como una distribución normal), y tenemos las calificaciones de varios estudiantes, podemos usar los intervalos de predicción para estimar la calificación del siguiente estudiante.
En términos más sencillos, un intervalo de predicción es como decir: "Basado en lo que hemos visto hasta ahora, la próxima vez que observemos esto, esperamos que el resultado esté entre este valor y este otro valor".
Este concepto no solo se aplica a una sola observación futura. También se puede usar para situaciones más complejas, como predecir la inundación más grande que podría ocurrir en un río en los próximos 50 años, basándose en datos históricos.
Algunos expertos en estadística prefieren los intervalos de predicción porque se centran en lo que podemos observar (datos pasados y futuros), en lugar de en características de una población que no podemos ver directamente.
Intervalos de predicción con datos normales
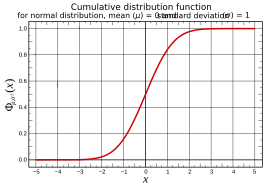
Cuando los datos que tenemos siguen una distribución normal (una forma de campana en un gráfico), y no conocemos exactamente sus características (como el promedio o la dispersión), podemos calcular intervalos de predicción. Esto significa que podemos encontrar un rango de valores donde la próxima observación caerá un cierto porcentaje de veces si repetimos el experimento.
Cuando conocemos el promedio y la dispersión
Si conocemos el promedio (media) y la dispersión (varianza o desviación estándar) de un grupo de datos, es más fácil calcular un intervalo de predicción.
Por ejemplo, si sabemos que las alturas de los estudiantes en una escuela tienen un promedio de 160 cm y una desviación estándar de 10 cm, podemos predecir que el 95% de los estudiantes tendrán una altura entre 140 cm y 180 cm. Esto se calcula usando una tabla especial (la tabla Z) que nos dice qué tan lejos del promedio se encuentran la mayoría de los datos.
| Intervalo de Predicción |
z |
|---|---|
| 75% | 1.15 |
| 90% | 1.64 |
| 95% | 1.96 |
| 99% | 2.58 |
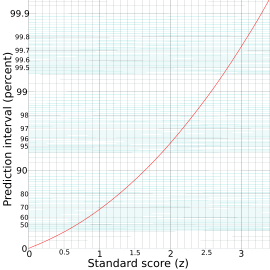
El intervalo de predicción se escribe así:
Por ejemplo, para un intervalo de predicción del 95% en una distribución con promedio (µ) de 5 y desviación estándar (σ) de 1, el valor de z es aproximadamente 2 (según la tabla). Entonces, el límite inferior sería 5 - (2 * 1) = 3, y el límite superior sería 5 + (2 * 1) = 7. Esto nos da un intervalo de [3, 7].
Cuando no conocemos los parámetros
En la vida real, casi nunca conocemos el promedio o la dispersión exactos de una población. Por eso, tenemos que estimarlos a partir de los datos que sí tenemos (nuestra muestra).
Cuando usamos estimaciones en lugar de los valores exactos, nuestros intervalos de predicción son un poco más amplios. Esto se debe a que hay más incertidumbre, ya que no solo estamos prediciendo un valor futuro, sino que también estamos adivinando los parámetros del grupo.
Si no conocemos el promedio, la dispersión, o ambos, usamos cálculos más complejos que tienen en cuenta esta incertidumbre. Esto nos lleva a usar una distribución diferente, llamada "t de Student", que es más adecuada para cuando trabajamos con muestras pequeñas o con parámetros desconocidos.
Métodos sin suposiciones (no paramétricos)
A veces, no podemos asumir que nuestros datos siguen una distribución normal o cualquier otro patrón específico. En estos casos, podemos usar métodos "no paramétricos" para calcular intervalos de predicción.
Imagina que tienes dos números al azar, X1 y X2. La probabilidad de que X2 sea mayor que X1 es del 50%, sin importar de dónde vengan esos números. Esto significa que si tomas un número, el 50% de las veces el siguiente número será mayor.
De manera similar, si tienes un grupo de números (X1, ..., Xn), la probabilidad de que la siguiente observación (Xn+1) sea la más grande de todas es 1 dividido por (n+1). La probabilidad de que sea la más pequeña también es 1 dividido por (n+1).
Esto significa que la mayor parte del tiempo, la siguiente observación caerá entre el valor más pequeño y el más grande que ya hemos visto. Por ejemplo, si tienes 19 observaciones, la probabilidad de que la vigésima observación caiga entre la más pequeña y la más grande de las 19 es del 90%.
Este método es útil porque no requiere que los datos sigan un patrón específico, lo que lo hace muy flexible.
Diferencias con otros intervalos
Intervalos de predicción vs. intervalos de confianza
Es importante recordar la diferencia clave:
- Un intervalo de predicción te dice dónde es probable que caiga una *observación futura individual*.
- Un intervalo de confianza te da un rango para el valor de una *característica de un grupo grande* (como el promedio de todas las personas en un país).
Los intervalos de predicción usan los datos que ya tenemos para estimar directamente el resultado de una nueva observación. Los intervalos de confianza, en cambio, usan los datos para estimar los parámetros del grupo, y luego, si queremos predecir, asumimos que la nueva observación vendrá de ese grupo estimado.
Intervalos de predicción vs. intervalos de tolerancia
Un intervalo de tolerancia es un rango que, con cierta confianza, contiene una proporción específica de una población. Por ejemplo, un intervalo de tolerancia podría decir que el 95% de los estudiantes de una escuela tienen una altura entre 150 cm y 170 cm. Es más sobre la población en general que sobre una observación futura específica.
Usos de los intervalos de predicción
Los intervalos de predicción se usan comúnmente para establecer rangos de referencia. Por ejemplo, en los exámenes de sangre, se usan para determinar si los resultados de una persona son "normales" o no. El intervalo de predicción del 95% es muy común para esto, y se le llama "rango de referencia estándar".
En el análisis de regresión
Una aplicación muy común es en el análisis de la regresión. Aquí, intentamos encontrar una línea o curva que mejor se ajuste a nuestros datos para predecir valores.
Por ejemplo, si estamos modelando cómo el número de horas de estudio afecta la calificación de un examen, la regresión lineal nos da una línea que predice la calificación promedio para un cierto número de horas de estudio. Un intervalo de predicción nos diría un rango donde la calificación *real* de un estudiante específico probablemente caería, dado un número de horas de estudio. Este rango es más amplio que solo la predicción de la línea, porque tiene en cuenta la variabilidad natural de los resultados.
Enfoque bayesiano
En la estadística bayesiana, también se pueden calcular intervalos de predicción. Estos se basan en la "probabilidad a posteriori" de una variable, que es una forma de actualizar nuestras creencias sobre algo a medida que obtenemos más datos. Aunque a menudo se usan para estimar parámetros, también son muy útiles para predecir eventos futuros, especialmente cuando se trata de valores extremos que aún no se han observado.
Ver también
- Extrapolación (matemática)
- Predicción
Véase también
 En inglés: Prediction interval Facts for Kids
En inglés: Prediction interval Facts for Kids


![\left[\mu- z\sigma,\ \mu + z\sigma \right].](/images/math/2/3/5/2354d60e9bf54f90c38401a2a3a3ba11.png)