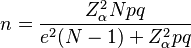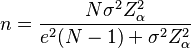Tamaño de la muestra para Niños

En estadística, el tamaño de la muestra es la cantidad de personas o elementos que elegimos de un grupo más grande, llamado población, para estudiar. Es importante que esta cantidad sea la correcta para que los resultados que obtengamos sean útiles y representen bien a todo el grupo.

Contenido

¿Por qué es importante elegir bien el tamaño de la muestra?
Cómo calcular el tamaño de la muestra
Estimar valores en la población
- Estimar una proporción
- Estimar un promedio
Comparar ideas o hipótesis
- Comparar dos proporciones
Véase también

¿Por qué es importante elegir bien el tamaño de la muestra?

Elegir el tamaño adecuado de una muestra es clave por varias razones:

Para entender un dato específico: Nos ayuda a calcular un valor importante de la población con la confianza que necesitamos.
Para encontrar diferencias: Permite descubrir si hay diferencias reales entre distintos grupos que estamos comparando.
Para ahorrar recursos: Un tamaño de muestra correcto puede hacer que el estudio sea más rápido y menos costoso.

Por ejemplo, en un estudio de investigación, si la muestra es muy pequeña, podríamos no ver diferencias importantes entre los grupos, lo que nos llevaría a conclusiones equivocadas. Sería como intentar saber qué piensa toda una escuela preguntando solo a dos estudiantes.

Por otro lado, si la muestra es demasiado grande, el estudio puede volverse muy caro y llevar mucho tiempo. Además, no es bueno pedir a más personas de las necesarias que participen en algo que quizás no les beneficie.

El tamaño de una muestra es simplemente el número de individuos que la forman.

Cómo calcular el tamaño de la muestra

Existen fórmulas para calcular el tamaño de la muestra, dependiendo de si conocemos o no ciertos datos de la población.

Cuando no conocemos la variabilidad de la población

Si no sabemos qué tan variados son los datos en la población, podemos usar una fórmula para tener una idea del tamaño de la muestra necesario:

n=\frac{{Z}^{2}_{\alpha}Npq}{e^2(N-1)+{Z}^{2}_{\alpha}pq}

Aquí te explicamos qué significa cada letra:

N: Es el tamaño total de la población, es decir, el número completo de personas o cosas que podríamos estudiar.
Z_α: Es un número que depende de qué tan seguros queremos estar de nuestros resultados (nivel de confianza). Por ejemplo, si queremos estar 95% seguros, este valor suele ser 1.96.
e: Es el error que estamos dispuestos a aceptar. Es la diferencia máxima que podría haber entre el resultado de nuestra muestra y el resultado real de toda la población. Por ejemplo, si decimos que el 60% de las personas están satisfechas con un error del 3%, significa que el porcentaje real está entre el 57% y el 63%.
p: Es la proporción de personas en la población que tienen la característica que nos interesa. Si no lo sabemos, lo más seguro es usar 0.5 (o 50%).
q: Es la proporción de personas que no tienen esa característica. Se calcula como 1 menos p (1-p).
n: Es el tamaño de la muestra que necesitamos calcular.

Es importante recordar que tener un nivel de confianza muy alto y un error muy bajo no garantiza que la encuesta sea perfecta. Lo más importante es recoger los datos de forma correcta.

Cuando conocemos la variabilidad de la población

Si ya tenemos una idea de la variabilidad de los datos en la población (por ejemplo, por estudios anteriores), usamos una fórmula un poco diferente:

n={{N\sigma^{2}Z^{2}_{\alpha}} \over {e^2(N-1)+\sigma^{2}Z^{2}_{\alpha}}}

En esta fórmula:

n: Es el tamaño de la muestra.
N: Es el tamaño de la población.
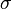$\sigma$ : Es la desviación estándar de la población, que nos dice qué tan dispersos están los datos. Si no la conocemos, podemos estimarla.
Z_α: Es el valor que depende del nivel de confianza, como en la fórmula anterior.
e: Es el límite de error que aceptamos.

Por ejemplo, si tenemos una población de 500 elementos y queremos un nivel de confianza del 95%, y estimamos la desviación estándar en 0.5 y el error en 0.05, el cálculo nos daría un tamaño de muestra de aproximadamente 218.

¿Qué pasa si la población es muy grande o desconocida?

Cuando la población es tan grande que parece infinita o simplemente no sabemos su tamaño exacto, las fórmulas se simplifican. En estos casos, el tamaño de la muestra suele ser:

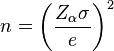
n=\biggl({\frac{Z_{\alpha}\sigma}{e}}\biggr)^2

Y si además no conocemos la proporción de la característica que estudiamos (p=q=0.5), la fórmula se vuelve aún más sencilla:

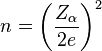
n=\biggl({\frac{Z_{\alpha}}{2e}}\biggr)^2

Estas fórmulas simplificadas nos dan un tamaño de muestra que es seguro (quizás un poco más grande de lo necesario, pero nunca insuficiente).

Estimar valores en la población

La estimación de parámetros es como adivinar un valor en la población grande, usando lo que aprendemos de nuestra muestra. Para esto, necesitamos entender conceptos como el nivel de confianza y el error.

Estimar una proporción

Para calcular cuántos sujetos necesitamos para estimar una proporción (por ejemplo, qué porcentaje de personas prefiere un color), necesitamos saber:

Z_α/2: Un valor que depende del riesgo que estamos dispuestos a aceptar (normalmente 1.96 para un riesgo del 5%).
P: La proporción que creemos que existe en la población.
i: La precisión con la que queremos que sea nuestra estimación.

Estimar un promedio

Para calcular cuántos sujetos necesitamos para estimar un promedio (por ejemplo, la altura promedio de los estudiantes), necesitamos:

Z_α/2: El mismo valor Z que antes.
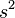$s^2$ : La varianza de la variable que estamos estudiando en la población.
i: La precisión deseada para nuestra estimación.

Comparar ideas o hipótesis

Cuando queremos ver si hay diferencias entre dos ideas o hipótesis en un estudio, también necesitamos calcular el tamaño de la muestra. Para esto, consideramos:

Errores de tipo I y tipo II: Son los riesgos de equivocarnos al sacar conclusiones. Queremos que estos riesgos sean bajos.
Si la hipótesis es de una o dos direcciones: Una hipótesis "de dos colas" (que busca diferencias en cualquier dirección) requiere una muestra más grande.
La magnitud de la diferencia: Si esperamos una diferencia grande, necesitaremos una muestra más pequeña. Si la diferencia es muy sutil, la muestra deberá ser mayor.
La variabilidad: Qué tan diferentes son los datos en la población.

Comparar dos proporciones

Para comparar dos proporciones (por ejemplo, si un nuevo tratamiento es mejor que uno antiguo), necesitamos definir valores como:

1.645 o 1.96: Valores Z para diferentes niveles de riesgo.
Proporciones esperadas: Los porcentajes que esperamos ver en cada grupo (por ejemplo, el grupo de control y el grupo con el nuevo tratamiento).

Véase también

En inglés: Sample size determination Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Tamaño_de_la_muestra&oldid=4982909»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Tamaño de la muestra para Niños. Enciclopedia Kiddle.

Tamaño de la muestra para niños