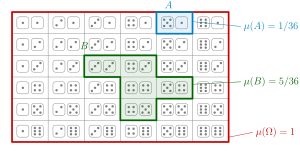
Espacio de probabilidad para niños

Enciclopedia para niños

Un espacio de probabilidad es una idea matemática que nos ayuda a entender y predecir lo que puede pasar en un experimento aleatorio. Imagina que lanzas una moneda o un dado; no sabes el resultado exacto, pero puedes calcular las posibilidades.

Este concepto fue presentado por el matemático Andréi Kolmogórov en 1933, y es fundamental en la teoría de probabilidades.

Un espacio de probabilidad tiene tres partes principales:

Un espacio muestral (se escribe con el símbolo 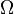$\Omega$ ): Es la lista de todos los resultados posibles de un experimento. Por ejemplo, si lanzas un dado, los resultados posibles son {1, 2, 3, 4, 5, 6}.
Un espacio de sucesos (se escribe con el símbolo 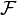$\mathcal{F}$ ): Es un grupo de eventos. Un evento es un conjunto de uno o más resultados del espacio muestral. Por ejemplo, en el lanzamiento de un dado, un evento podría ser "sacar un número par", que incluye los resultados {2, 4, 6}.
Una función de probabilidad (se escribe con el símbolo $P$ ): Es una regla que le da un número entre 0 y 1 a cada evento. Este número nos dice qué tan probable es que ese evento ocurra. Un 0 significa que es imposible, y un 1 significa que es seguro.

Para que este modelo funcione bien, estas tres partes deben seguir algunas reglas básicas, llamadas axiomas.

Cuando realizamos un experimento, es como si la "naturaleza" eligiera uno de los resultados posibles del espacio muestral. Los eventos que incluyen ese resultado se consideran "ocurridos". Si repetimos el experimento muchas veces, la cantidad de veces que ocurre un evento, comparada con el total de experimentos, se acercará mucho a la probabilidad que le asignamos.

Contenido

¿Qué es un Espacio de Probabilidad?
Partes de un Espacio de Probabilidad
- Consecuencias Importantes
Ejemplos de Espacios de Probabilidad
Galería de imágenes
Véase también

¿Qué es un Espacio de Probabilidad?

Espacio de probabilidad para lanzar un dado dos veces seguidas: El espacio muestral

\Omega

tiene 36 resultados posibles. Se muestran tres eventos diferentes (áreas de colores) con sus probabilidades.

Un espacio de probabilidad es como un conjunto de herramientas matemáticas $(\Omega, \mathcal{F}, P)$ que usamos para crear un modelo de situaciones reales. Quien crea el modelo decide qué resultados, eventos y probabilidades incluirá.

El Espacio Muestral: Todos los Resultados Posibles

El espacio muestral 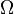$\Omega$ es el conjunto de todos los resultados que pueden ocurrir en un experimento. Cada vez que realizamos el experimento, obtenemos un solo resultado. Si los resultados son diferentes de alguna manera importante, se consideran resultados distintos. Por ejemplo, al lanzar una moneda, el espacio muestral es {Cara, Cruz}.

El Espacio de Sucesos: Los Eventos que Nos Interesan

El σ-álgebra 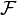$\mathcal{F}$ es una colección de todos los eventos que queremos estudiar. Un "evento" es un grupo de uno o más resultados del espacio muestral. Decimos que un evento "ha ocurrido" si el resultado del experimento es parte de ese evento.

Por ejemplo, si lanzamos dos dados, un evento podría ser "la suma de los puntos es 7". Otro evento podría ser "el primer dado es un número par". Si el resultado es que el primer dado cae en 2 y el segundo en 5, entonces ambos eventos ("suma 7" y "primer dado par") han ocurrido.

La Función de Probabilidad: Asignando Posibilidades

La medida de probabilidad $P$ es una función que nos dice la probabilidad de un evento. Una probabilidad es un número entre 0 y 1.

0 significa que el evento es imposible.
1 significa que el evento es seguro que ocurrirá.

La función de probabilidad debe cumplir dos reglas importantes:

La probabilidad de que ocurra uno de varios eventos que no pueden pasar al mismo tiempo (eventos mutuamente excluyentes) es la suma de sus probabilidades individuales. Por ejemplo, al lanzar una moneda, la probabilidad de que salga "Cara" o "Cruz" es la suma de la probabilidad de "Cara" más la probabilidad de "Cruz".
La probabilidad de que ocurra algún resultado del espacio muestral completo es 1. Esto significa que siempre ocurrirá algo. En el ejemplo de la moneda, la probabilidad de que salga "Cara" o "Cruz" es 1, porque es seguro que saldrá una de las dos.

No todos los grupos de resultados en el espacio muestral son necesariamente eventos que nos interesen o que podamos "medir" su probabilidad. Por ejemplo, en un lanzamiento de jabalina, nos interesan eventos como "la jabalina cae entre 60 y 65 metros", pero no "la jabalina cae a una distancia que es un número irracional".

Partes de un Espacio de Probabilidad

Un espacio de probabilidad se define formalmente como una terna 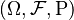$(\Omega , \mathcal{F},\operatorname{P} )$ donde:

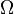$\Omega$ es el espacio muestral, el conjunto de todos los resultados posibles.
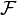es una σ-álgebra de subconjuntos de 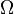. Esto significa que 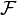es una colección de eventos que cumple ciertas propiedades:
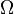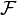- El espacio muestral completo $\Omega$ es un evento en $\mathcal{F}$ .
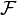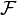- Si un evento $A$ está en $\mathcal{F}$ , entonces su complemento (todo lo que no es $A$ ) también está en $\mathcal{F}$ .
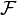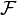- Si tienes varios eventos en $\mathcal{F}$ , la unión de esos eventos (cuando ocurre al menos uno de ellos) también está en $\mathcal{F}$ .
es la medida de probabilidad o función de probabilidad. Esta función asigna una probabilidad a cada evento y sigue los axiomas de Kolmogorov:
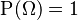- La probabilidad de todo el espacio muestral es 1: $\operatorname{P}(\Omega)=1$ .
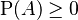- La probabilidad de cualquier evento es siempre mayor o igual a 0: $\operatorname{P}(A)\geq0$ .
- Si tienes varios eventos que no pueden ocurrir al mismo tiempo (son disjuntos), la probabilidad de que ocurra cualquiera de ellos es la suma de sus probabilidades individuales.

Consecuencias Importantes

De estas reglas básicas se pueden deducir otras propiedades:

La probabilidad de que ocurra el conjunto vacío (es decir, que no ocurra nada) es 0: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{P}(\emptyset)=0 .
Si tienes dos eventos $A$ y $B$ , la probabilidad de que ocurra $A$ o $B$ (o ambos) es la suma de sus probabilidades menos la probabilidad de que ocurran ambos: $\operatorname{P}[A\cup B]=\operatorname{P}[A]+\operatorname{P}[B]-\operatorname{P}[A\cap B]$ .

Ejemplos de Espacios de Probabilidad

Aquí te mostramos algunos ejemplos para entender mejor:

Lanzamiento de una Moneda

Si lanzamos una moneda justa una sola vez:

El espacio muestral 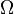$\Omega$ es {Cara, Cruz}.
El espacio de sucesos 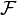$\mathcal{F}$ incluye todos los posibles grupos de resultados: {}, {Cara}, {Cruz}, {Cara, Cruz}.
La función de probabilidad asigna:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(\{\}) = 0 (imposible no obtener nada)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(\{\text{Cara}\}) = 0.5 (50% de probabilidad de cara)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(\{\text{Cruz}\}) = 0.5 (50% de probabilidad de cruz)
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(\{\text{Cara}, \text{Cruz}\}) = 1 (seguro que sale cara o cruz)

Tres Lanzamientos de Moneda

Si lanzamos una moneda tres veces, hay 8 resultados posibles en el espacio muestral 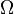$\Omega$ : {CCC, CCX, CXC, CXX, XCC, XCX, XXC, XXX}. (Aquí, "CXC" significa Cara en el primer lanzamiento, Cruz en el segundo y Cara en el tercero).

Podemos definir diferentes espacios de sucesos dependiendo de la información que tengamos:

Si solo sabes el resultado del segundo lanzamiento, tu espacio de sucesos sería más limitado.
Si solo sabes el número total de cruces, tu espacio de sucesos también sería diferente.

Encuesta a Votantes

Imagina que se eligen al azar 100 votantes de California para preguntarles por quién votarán como gobernador. El espacio muestral 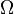$\Omega$ sería el conjunto de todas las posibles secuencias de 100 votantes diferentes.

Si solo te interesa saber si un candidato específico recibió al menos 60 votos, tu espacio de sucesos sería simple: un evento para "al menos 60 votos" y otro para "menos de 60 votos".
Si conoces el número exacto de votos que recibió el candidato, tu espacio de sucesos sería mucho más detallado, con un evento para cada posible número de votos (de 0 a 100).

Galería de imágenes

Espacio de probabilidad para lanzar un dado dos veces seguidas: El espacio muestral $\Omega$ tiene 36 resultados posibles. Se muestran tres eventos diferentes (áreas de colores) con sus probabilidades.

Véase también

En inglés: Probability space Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Espacio_de_probabilidad&oldid=4747330»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Espacio de probabilidad para Niños. Enciclopedia Kiddle.