Divergencia (matemática) para niños
La divergencia es una idea matemática que nos ayuda a entender cómo se mueve algo, como el agua o el aire, en un espacio. Imagina que tienes un punto en un río. La divergencia te diría si el agua se está esparciendo desde ese punto (como si hubiera una fuente) o si se está juntando hacia él (como si hubiera un sumidero).
Si la divergencia es positiva, significa que algo se está "creando" o "saliendo" de un lugar. Si es negativa, algo se está "consumiendo" o "entrando". Si es cero, el flujo es "incompresible", lo que significa que no se crea ni se destruye nada en ese punto. A los campos con divergencia cero se les llama también campos solenoidales.
Contenido
¿Qué es la divergencia de un campo vectorial?
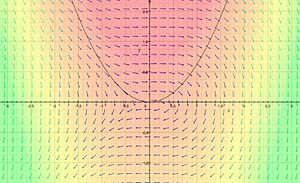
La divergencia se aplica a los campos vectoriales. Un campo vectorial es como un mapa donde en cada punto hay una flecha que indica una dirección y una fuerza. Por ejemplo, un mapa de vientos es un campo vectorial: en cada lugar, una flecha muestra hacia dónde sopla el viento y con qué fuerza.
La divergencia de un campo vectorial en un punto específico nos dice cuánto "fluye" o "sale" de ese punto por unidad de volumen. Es como si midiéramos la cantidad neta de algo que se aleja o se acerca a un lugar muy pequeño.
Fuentes y sumideros en los campos
Si la divergencia en un punto es positiva, decimos que el campo tiene una "fuente" allí. Piensa en un grifo abierto: el agua sale de él, es una fuente.
Si la divergencia es negativa, el campo tiene un "sumidero". Imagina un desagüe: el agua entra en él, es un sumidero.
Un ejemplo común son las cargas eléctricas. Las cargas positivas actúan como "fuentes" para el campo eléctrico, y las cargas negativas son "sumideros".
¿Cómo se calcula la divergencia?
Calcular la divergencia implica usar derivadas parciales, que son una forma de medir cómo cambia una función en una dirección específica.
En un espacio tridimensional, como el que vivimos, si un campo vectorial se describe con componentes en las direcciones X, Y y Z, la divergencia se calcula sumando cómo cambia cada componente en su propia dirección.
Divergencia en diferentes sistemas de coordenadas
La forma de calcular la divergencia puede variar dependiendo del sistema de coordenadas que usemos para describir el espacio. Los sistemas más comunes son:
- Coordenadas cartesianas: Son las coordenadas X, Y, Z que usamos normalmente.
- Coordenadas cilíndricas: Útiles para problemas con simetría cilíndrica, como el flujo de agua en una tubería. Usan una distancia al eje central, un ángulo y una altura.
- Coordenadas esféricas: Ideales para problemas con simetría esférica, como el campo de gravedad alrededor de un planeta. Usan una distancia al centro, y dos ángulos.
Aunque las fórmulas matemáticas cambian para cada sistema, la idea de la divergencia sigue siendo la misma: medir el flujo neto hacia afuera o hacia adentro de un punto.
Propiedades importantes de la divergencia
La divergencia tiene algunas propiedades que la hacen muy útil en física e ingeniería:
- Es lineal: Si sumas dos campos vectoriales y calculas su divergencia, es lo mismo que calcular la divergencia de cada uno por separado y luego sumarlas.
- Relación con el rotacional: La divergencia de un campo que ya es el "rotacional" de otro campo siempre es cero. El rotacional mide la tendencia de un campo a girar.
El teorema de la divergencia
El teorema de la divergencia, también conocido como teorema de Gauss, es una herramienta muy poderosa. Relaciona la divergencia de un campo vectorial dentro de un volumen con el flujo total de ese campo a través de la superficie que encierra ese volumen.
Imagina que tienes una caja (el volumen) y quieres saber cuánto aire sale de ella. El teorema de la divergencia te dice que puedes calcularlo de dos maneras:
- Midiendo el aire que atraviesa cada parte de la superficie de la caja.
- Calculando la divergencia del campo de aire en cada punto dentro de la caja y sumando esos valores.
Este teorema es fundamental en áreas como la electrostática (cómo se comportan las cargas eléctricas) y la mecánica de fluidos (cómo se mueven los líquidos y gases).
Véase también
 En inglés: Divergence Facts for Kids
En inglés: Divergence Facts for Kids
- Rotacional
- Gradiente
- Teorema de la divergencia