robot de la enciclopedia para niños

Desplazamiento (vector) para niños

Enciclopedia para niños
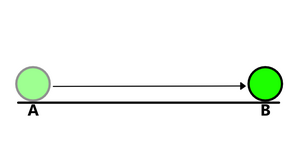
Archivo:Deslocamento
La esfera se movió del punto A al punto B

En mecánica, el desplazamiento es el vector que define la posición de un punto o partícula en relación con un origen A con respecto a una posición B. El vector se extiende desde el punto de referencia hasta la posición final.

Introducción

En la dinámica del punto material, se entiende por desplazamiento el vector o segmento recto orientado que une la posición inicial con otro punto genérico de la trayectoria. Este uso del vector desplazamiento permite describir en forma completa el movimiento y el camino de una partícula.

En mecánica de medios continuos se entiende por desplazamiento el vector que va desde la posición inicial (antes de la deformación) a la final (después de la deformación) de un mismo punto material del medio continuo.

Cuando el punto de referencia es el origen del sistema de coordenadas que se utiliza, el vector desplazamiento se denomina por lo general vector posición, que indica la posición por medio de la línea recta dirigida desde la posición previa a la posición actual, en comparación con la magnitud escalar "distancia recorrida" que indica solo la longitud del camino, obviamente en un espacio euclídeo se tiene:

\|\Delta\mathbf{r}(t)\| \le L_r = \int_0^t v(t)\ dt = \int_0^t \left\| \frac{d\mathbf{r}(t)}{dt} \right\|\ dt

La igualdad anterior solo se cumpliría para un movimiento rectilíneo.

Cuando el punto de referencia es la posición previa de la partícula, el vector desplazamiento indica la dirección del movimiento por medio de un vector que va desde la posición previa a la posición actual. Este uso del vector desplazamiento es útil para definir a los vectores velocidad y aceleración de una partícula definida.

Desplazamientos de puntos materiales aislados

En ciertos contextos se representa por Δx y viene dado por:

\Delta_x(t) = x_t - x_0\,

Desplazamientos en un sólido deformable

Si llamamos K a la región del espacio ocupada por un sólido deformable podemos representar el proceso de deformación entre dos posiciones como un difeomorfismo T_D: K \to \mathbb{R}^3 . Si consideramos un sistema de coordenadas cartesianas (x, y, z) sobre K se define el vector desplazamiento u para cada punto sencillamente como:

\mathbf{u} = (u_x, u_y, u_z) = T_D(x,y,z) - (x,y,z)\,

A partir de este vector de desplazamientos es trivial calcular las componentes de la deformación y si se conoce la ley constitutiva del sólido deformable pueden determinarse las tensiones mecánicas a que se halla sometido. En concreto el tensor deformación de Green-Lagrange:

\mathbf{D} = (\varepsilon_{ij}), \quad \mbox{donde}\ \varepsilon_{ij} = {1 \over 2} \left ({\partial u_i \over \partial x_j} + {\partial u_j \over \partial x_i}+\sum_{k}{\partial u_k \over \partial x_i}{\partial u_k \over \partial x_j}\right)

Donde:

\begin{matrix} u_1 := u_x & u_2 := u_y & u_3 := u_z\\ x_1 := x & x_2 := y & x_3 := z \end{matrix}

Véase también

Kids robot.svg En inglés: Displacement (geometry) Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Desplazamiento_(vector)&oldid=4069222»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Desplazamiento (vector) para Niños. Enciclopedia Kiddle.