Cuerda que rodea la Tierra para niños
El problema de la cuerda que rodea la Tierra es un divertido acertijo de matemáticas que tiene una respuesta que parece ir en contra de lo que esperaríamos. Imagina que tienes una cuerda que rodea perfectamente el ecuador de la Tierra, como si fuera un cinturón. La Tierra, para este problema, se considera una esfera perfecta.
Ahora, cortas esa cuerda y le añades un trozo extra de solo 1 metro de largo. Después, vuelves a colocar la cuerda alrededor de la Tierra, pero esta vez la levantas para que quede a la misma altura en todos los puntos sobre el ecuador. La pregunta es: ¿cuánto espacio habrá entre la cuerda y el suelo? ¿Será suficiente para que pase un coche, un gato o solo la hoja de un cuchillo?
Contenido
El Misterio de la Cuerda Alrededor de la Tierra
A primera vista, podrías pensar que añadir solo 1 metro a una cuerda que ya mide unos 40.000 kilómetros (la circunferencia de la Tierra) no hará mucha diferencia. Parece que la cuerda apenas se levantaría del suelo. Sin embargo, la solución es muy sorprendente.
La Sorprendente Solución Matemática
La respuesta correcta es que la cuerda se levantará lo suficiente como para que un gato pueda pasar fácilmente por debajo. La separación entre la cuerda y el suelo será de aproximadamente 16 centímetros. ¡Es mucho más de lo que la mayoría de la gente espera!
¿Cómo se Calcula la Separación?
Para entender por qué ocurre esto, podemos usar un poco de matemáticas. No te preocupes, es más sencillo de lo que parece.
Imagina que:
- C es la circunferencia original de la Tierra (o de cualquier círculo).
- R es el radio de la Tierra (la distancia desde el centro hasta la superficie).
- c es la longitud que le añadimos a la cuerda (en nuestro caso, 1 metro).
- r es el aumento del radio, es decir, la altura a la que se levanta la cuerda del suelo.
Sabemos que la circunferencia de un círculo se calcula con la fórmula: 2 π veces el radio (2πR).
Cuando añadimos el trozo de cuerda, la nueva circunferencia será C + c. Y el nuevo radio será R + r. Así que, la nueva circunferencia también se puede escribir como 2π(R + r).
Entonces, podemos igualar las dos formas de escribir la nueva circunferencia:
- C + c = 2π(R + r)
Ahora, sabemos que C es igual a 2πR (la circunferencia original). Sustituimos C en la ecuación:
- 2πR + c = 2πR + 2πr
Si restamos 2πR de ambos lados de la ecuación, ¡se cancela!
- c = 2πr
Para encontrar la altura (r), solo tenemos que despejar 'r':
- r = c / (2π)
Si 'c' es 1 metro, entonces:
- r = 1 / (2π) metros
Como π (pi) es aproximadamente 3.14159, 2π es aproximadamente 6.283.
- r = 1 / 6.283 metros
- r ≈ 0.159 metros, que es aproximadamente 16 centímetros.
¿Por Qué el Tamaño No Importa?
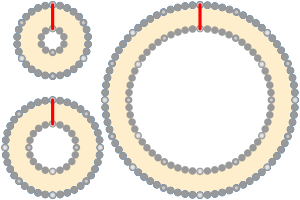
Lo más sorprendente de este problema es que el tamaño del círculo o esfera alrededor del cual se extiende la cuerda ¡no importa en absoluto! El resultado siempre será de unos 16 centímetros, ya sea que la cuerda rodee una pelota de baloncesto, un átomo o incluso una galaxia entera como la Vía Láctea. La fórmula r = c / (2π) no incluye el radio original (R), lo que significa que la altura extra (r) solo depende de la longitud añadida (c).
Ejemplos Curiosos de Este Principio
Este mismo principio se aplica en otros lugares. Por ejemplo, en una pista de atletismo, las líneas de salida para cada carril están escalonadas. La distancia que se adelanta cada línea es siempre la misma, sin importar si la pista es pequeña o grande. Esa distancia es igual a 2π veces el ancho del carril. Esto asegura que todos los corredores recorran la misma distancia si se mantienen en su carril.
Véase también
 En inglés: String girdling Earth Facts for Kids
En inglés: String girdling Earth Facts for Kids
- Problema del servilletero, otro problema matemático donde el tamaño de una esfera no es importante para la solución.