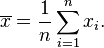Corrección de Bessel para niños
En estadística, la corrección de Bessel es una forma especial de ajustar los cálculos cuando trabajamos con datos. Lleva el nombre de Friedrich Bessel, un astrónomo y matemático alemán que vivió hace mucho tiempo (1784-1846).
Esta corrección consiste en usar el número (n − 1) en lugar de n en las fórmulas para calcular la varianza y la desviación estándar de una muestra. Aquí, n representa la cantidad de datos que tenemos en nuestra muestra. Al hacer este cambio, se logra que las estimaciones sean más precisas, especialmente cuando tenemos pocos datos.
Contenido
¿Qué son la población y la muestra?
Para entender la corrección de Bessel, primero debemos saber qué significan "población" y "muestra" en estadística.
La población: el grupo completo
Una población es el grupo completo de cosas o personas que nos interesan. Por ejemplo, si queremos saber la estatura de todos los estudiantes de 12 años en un país, la población sería todos esos estudiantes. Es un grupo muy grande.
La muestra: un pedacito de la población
Una muestra es un grupo más pequeño que tomamos de esa población. Por ejemplo, si no podemos medir a todos los estudiantes del país, podríamos medir a los estudiantes de 12 años de algunos colegios. Esa sería nuestra muestra. Usamos la muestra para tratar de entender cómo es la población completa.
Friedrich Bessel, el científico que le dio nombre a esta corrección, estudiaba las estrellas y los planetas. Para saber cómo se movían (sus órbitas), solo podía hacer unas pocas observaciones. Esas pocas observaciones eran su "muestra" de datos, y necesitaba que sus cálculos fueran lo más exactos posible.
¿Por qué necesitamos la corrección de Bessel?
Cuando calculamos la varianza (que nos dice qué tan dispersos están los datos) usando una muestra, a veces el resultado es un poco más pequeño de lo que debería ser si tuviéramos los datos de toda la población. Esto se llama un "sesgo" o un error.
Bessel descubrió que si en lugar de dividir por n (el número de datos en la muestra) dividimos por (n − 1), el cálculo de la varianza se vuelve más exacto. Es como si al quitarle 1 a n, compensáramos el hecho de que estamos trabajando con una muestra pequeña y no con todos los datos de la población.
El problema de la subestimación
Imagina que quieres saber qué tan diferentes son las alturas de todos los árboles en un bosque (la población). No puedes medir todos los árboles, así que mides solo 5 árboles (la muestra).
Si calculas la dispersión de esas 5 alturas usando la fórmula normal (dividiendo por 5), el resultado tiende a ser un poco menor que la dispersión real de todos los árboles del bosque. Esto sucede porque la media de tu pequeña muestra siempre estará más cerca de los datos de esa muestra que la media real de todo el bosque. Al dividir por (n − 1), la corrección de Bessel ayuda a que la estimación de la dispersión sea más grande y, por lo tanto, más cercana a la realidad de la población.
¿Cuándo es más importante?
La corrección de Bessel es muy importante cuando trabajamos con muestras pequeñas, por ejemplo, si tenemos 10 datos o menos. A medida que el número de datos en la muestra es más grande, la diferencia entre usar n o (n − 1) se vuelve muy pequeña y casi no importa. Pero para las muestras pequeñas, como las que usaba Bessel en sus observaciones astronómicas, esta corrección es clave para obtener resultados más fiables.
Fórmulas básicas
Aquí te mostramos cómo se calculan la media y la varianza:
La media muestral
La media muestral es el promedio de todos los datos en tu muestra. Se calcula sumando todos los valores y dividiendo por el número de datos (n):
La varianza muestral sin corrección
Esta es la fórmula de la varianza que tiende a subestimar la varianza de la población:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): s_n^2 = \frac {1}{n} \sum_{i=1}^n \left(x_i - \overline{x} \right)^ 2
La varianza muestral con corrección de Bessel
Esta es la fórmula corregida, que nos da una estimación más precisa de la varianza de la población:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): s^2 = \frac {1}{n-1} \sum_{i=1}^n \left(x_i - \overline{x} \right)^ 2
Como puedes ver, la única diferencia es que en la fórmula corregida dividimos por (n − 1) en lugar de n.
Galería de imágenes
Véase también
 En inglés: Bessel's correction Facts for Kids
En inglés: Bessel's correction Facts for Kids
- Sesgo estadístico
- Desviación estándar