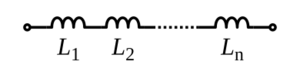Circuitos en serie y en paralelo para niños
Los componentes de un circuito eléctrico o electrónico se pueden conectar de varias maneras. Las dos formas más sencillas y comunes son el circuito en serie y el circuito en paralelo.
Cuando los componentes están conectados en serie, se unen a lo largo de una sola ruta. Esto significa que la misma corriente eléctrica fluye a través de todos ellos. Imagina una fila de personas tomadas de la mano: la energía pasa de una a otra en orden.
Si los componentes están conectados en paralelo, se unen a lo largo de múltiples rutas. En este caso, el mismo voltaje (la "fuerza" que empuja la corriente) se aplica a cada componente. Piensa en varias personas que reciben energía directamente de una misma fuente, cada una por su propio camino.
En un circuito en serie, la corriente es igual en cada parte, y el voltaje total del circuito es la suma de los voltajes de cada componente. En un circuito en paralelo, el voltaje es el mismo en cada componente, y la corriente total es la suma de las corrientes que pasan por cada uno.
Para entenderlo mejor, piensa en un circuito simple con cuatro bombillas y una batería de 6 voltios.
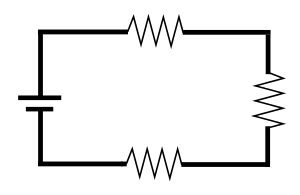
- Si un cable conecta la batería a la primera bombilla, luego a la segunda, a la tercera, a la cuarta y de vuelta a la batería, las bombillas están en serie. Si una bombilla se funde, el circuito se rompe y todas las bombillas se apagan.
- Si cada bombilla está conectada a la batería por su propio cable, formando un circuito separado para cada una, las bombillas están en paralelo. Si una bombilla se funde, las demás seguirán encendidas porque tienen sus propios caminos.
En el ejemplo de las bombillas en serie, la corriente es la misma en todas. El voltaje se divide entre ellas, por ejemplo, 1.5 voltios en cada una, lo que podría no ser suficiente para que brillen mucho. En cambio, si están en paralelo, cada bombilla recibe los 6 voltios completos de la batería y todas brillan con fuerza.
Contenido
Circuitos en serie: ¿Cómo funcionan?
Los circuitos en serie a veces se llaman "acoplados por corriente" o "en cadena". La corriente eléctrica fluye a través de cada componente uno tras otro. Esto significa que todos los componentes en una conexión en serie tienen la misma cantidad de corriente.
La característica principal de un circuito en serie es que solo tiene un camino para que la corriente fluya. Si este camino se interrumpe en cualquier punto, todo el circuito deja de funcionar. Por ejemplo, si una de las bombillas de una cadena de luces de Navidad antiguas se quema o se quita, toda la cadena se apaga hasta que se reemplaza la bombilla.
Corriente en serie
En los circuitos en serie, la corriente es la misma para todos los elementos. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): I = I_1 = I_2 = \cdots = I_n
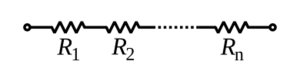
Resistencias en serie
La resistencia total de varias resistencias conectadas en serie es igual a la suma de sus resistencias individuales.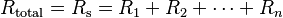 
Donde R_s es la resistencia en serie.
La conductancia eléctrica es lo contrario de la resistencia. La conductancia total de un circuito con resistencias en serie se calcula así: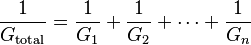 
Inductores en serie
Los inductores (componentes que almacenan energía en un campo magnético) siguen una regla similar. La inductancia total de inductores no acoplados en serie es la suma de sus inductancias individuales: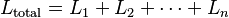 
Sin embargo, si los inductores están muy cerca y sus campos magnéticos se afectan entre sí, el cálculo se vuelve más complejo debido a la inductancia mutua.
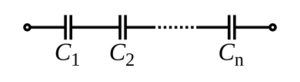
Condensadores en serie
Los condensadores (componentes que almacenan energía en un campo eléctrico) siguen una regla diferente. La capacitancia total de los condensadores en serie se calcula sumando los recíprocos de sus capacitancias individuales y luego tomando el recíproco de esa suma: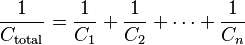 
Interruptores en serie
Dos o más interruptores conectados en serie funcionan como una compuerta lógica "Y" (AND). El circuito solo permitirá el paso de corriente si todos los interruptores están cerrados.
Celdas y baterías en serie
Una batería a menudo está formada por varias celdas conectadas en serie. Si las celdas se conectan en serie, el voltaje total de la batería será la suma de los voltajes de cada celda. Por ejemplo, una batería de coche de 12 voltios tiene seis celdas de 2 voltios conectadas en serie.
Voltaje en serie
En un circuito en serie, el voltaje total es la suma de todos los voltajes en los componentes individuales.
Circuitos en paralelo: ¿Cómo funcionan?
Si dos o más componentes están conectados en paralelo, tienen la misma diferencia de potencial (voltaje) en sus extremos. Esto significa que el mismo voltaje se aplica a todos los componentes conectados en paralelo. La corriente total que sale de la fuente es la suma de las corrientes que pasan por cada componente individual.
Voltaje en paralelo
En un circuito en paralelo, el voltaje es el mismo para todos los elementos. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = V_1 = V_2 = \ldots = V_n
Corriente en paralelo
La corriente total en un circuito paralelo se calcula así: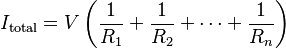 
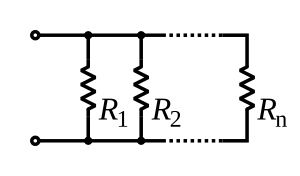
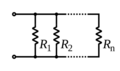
Resistencias en paralelo
Para encontrar la resistencia total de componentes en paralelo, se suman los recíprocos de las resistencias individuales y luego se toma el recíproco de esa suma. La resistencia total siempre será menor que la resistencia más pequeña de los componentes.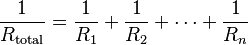 
Para solo dos resistencias, la fórmula simplificada es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): R_\mathrm{total} = \frac{R_1 R_2}{R_1 + R_2} Si hay N resistencias iguales en paralelo, la resistencia total es: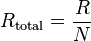 
La conductancia total de un circuito paralelo de resistencias es la suma de las conductancias individuales: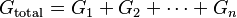 
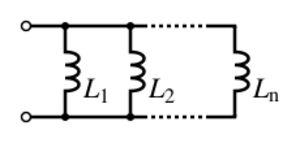
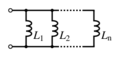
Inductores en paralelo
Los inductores en paralelo siguen una regla similar a las resistencias en paralelo. La inductancia total de inductores no acoplados en paralelo es el recíproco de la suma de los recíprocos de sus inductancias individuales: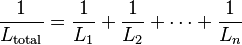 
Al igual que en serie, si los inductores están muy cerca y se afectan mutuamente, el cálculo se vuelve más complejo.
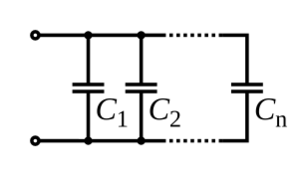
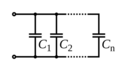
Condensadores en paralelo
La capacitancia total de los condensadores en paralelo es igual a la suma de sus capacitancias individuales: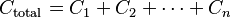 
El voltaje máximo que puede soportar una combinación de condensadores en paralelo está limitado por el condensador individual con el voltaje de trabajo más bajo.
Interruptores en paralelo
Dos o más interruptores en paralelo forman una compuerta lógica "O" (OR). El circuito transportará corriente si al menos uno de los interruptores está cerrado.
Celdas y baterías en paralelo
Si las celdas de una batería están conectadas en paralelo, el voltaje de la batería será el mismo que el voltaje de una sola celda. Sin embargo, la corriente total que puede suministrar la batería será la suma de las corrientes que puede dar cada celda. Por ejemplo, si una batería tiene cuatro celdas idénticas en paralelo y entrega 1 amperio, cada celda suministra 0.25 amperios. Las baterías de iones de litio, como las de los ordenadores portátiles, a menudo se conectan en paralelo para aumentar su capacidad de almacenamiento de energía (medida en amperios/hora).
Aplicaciones de los circuitos
Los circuitos en serie y paralelo se usan en muchas cosas que nos rodean:
- Baterías: Muchas baterías, como las de las linternas o herramientas eléctricas, usan celdas conectadas en serie para alcanzar el voltaje necesario. Por ejemplo, una batería de 48 voltios podría tener doce celdas de iones de litio en serie.
- Sistema circulatorio: En nuestro cuerpo, la sangre fluye a través de vasos sanguíneos que se pueden ver como resistencias en serie y paralelo. Dentro de un órgano, las arterias, arteriolas y capilares están en serie. Entre los órganos, las arterias que salen de la aorta están en paralelo, permitiendo que la sangre llegue a cada órgano por separado.
Galería de imágenes
-
Un circuito en serie con una fuente de voltaje (como una batería) y 3 resistencias.
-
Esquema de varias resistencias conectadas en serie.
-
Esquema de varios inductores conectados en serie.
-
Esquema de varios condensadores conectados en serie.
-
Esquema de varias resistencias conectadas en paralelo.
-
Esquema de varios inductores conectados en paralelo.
-
Esquema de varios condensadores conectados en paralelo.
Véase también
En inglés: Series and parallel circuits Facts for Kids
- Análisis de circuitos
- Divisor de tensión
- Divisor de corriente
