Capacidad eléctrica para niños
La capacidad eléctrica es una propiedad que tienen algunos objetos para guardar o almacenar carga eléctrica. Imagina que es como un pequeño "tanque" para la electricidad. Cuanto más grande es este "tanque", más carga eléctrica puede guardar.
El dispositivo más común que almacena energía de esta forma se llama condensador. Piensa en él como una batería muy rápida que puede cargarse y descargarse en un instante.
La relación entre la diferencia de potencial (también llamada voltaje, que es como la "presión" eléctrica) entre las partes de un condensador y la carga eléctrica que almacena se explica con esta fórmula:
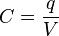
Donde:
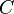es la capacidad, y se mide en faradios. Esta unidad es muy grande, por eso normalmente usamos unidades más pequeñas como el microfaradio (µF) o el picofaradio (pF). El faradio lleva el nombre de un científico llamado Michael Faraday.
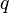es la carga eléctrica que se guarda, y se mide en culombios.
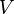es la diferencia de potencial o voltaje, y se mide en voltios.
La capacidad siempre es un número positivo. Depende de cómo esté hecho el condensador (su forma y tamaño) y del material que se ponga entre sus partes conductoras, llamado dieléctrico. Cuanto mejor sea el material dieléctrico para aislar, mayor será la capacidad del condensador.
Contenido
¿Cómo se almacena la energía en un condensador?
Un condensador no solo guarda carga, ¡también almacena energía! Esta energía se mide en julios. Para cargar un condensador, se necesita hacer un "trabajo" eléctrico, y parte de ese trabajo se guarda como energía potencial.
La energía almacenada en un condensador se puede calcular con esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): W_{almacenada} = \frac{1}{2} C V^2
Donde:
- W es la energía almacenada, en julios.
- C es la capacidad del condensador, en faradios.
- V es el voltaje o diferencia de potencial, en voltios.
Esta fórmula nos dice que cuanta más capacidad tenga un condensador o cuanto mayor sea el voltaje que se le aplique, más energía podrá almacenar.
Tipos de capacidad
Existen dos ideas principales de capacidad:
- Capacidad propia: Es la capacidad de un objeto para almacenar carga eléctrica por sí mismo, sin necesidad de otro objeto cerca. Por ejemplo, la Tierra tiene una capacidad propia muy grande.
- Capacidad mutua: Es la capacidad que se mide entre dos objetos, como las dos placas de un condensador. Esta es la más importante cuando hablamos de los condensadores que usamos en los circuitos.
La capacidad entre dos conductores (como las placas de un condensador) depende solo de su forma, el tamaño de sus superficies, la distancia entre ellas y el tipo de material dieléctrico que los separa.
Condensadores: Componentes clave
Los condensadores son componentes electrónicos muy comunes. La capacidad de la mayoría de los condensadores que se usan en los circuitos es mucho menor que un faradio. Por eso, se usan subunidades como:
- Microfaradio (µF): Un millón de veces más pequeño que un faradio.
- Nanofaradio (nF): Mil millones de veces más pequeño que un faradio.
- Picofaradio (pF): Un billón de veces más pequeño que un faradio.
Existen también los supercondensadores, que pueden almacenar mucha más energía, ¡hasta cientos de faradios!
La capacidad de un condensador se puede entender así: cuando pones carga positiva en un lado, esta carga crea un campo eléctrico que "empuja" a cualquier otra carga positiva que intente llegar. Pero si hay otro lado con carga negativa cerca, el campo eléctrico de la carga positiva se debilita un poco, haciendo más fácil añadir más carga. Por eso, la presencia de la otra placa con carga opuesta ayuda a que el condensador pueda almacenar más carga con el mismo voltaje.
Para un condensador de placas paralelas (dos láminas conductoras separadas por una distancia), la capacidad se calcula con una fórmula sencilla:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle \ C=\varepsilon\frac{A}{d}}
Donde:
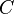es la capacidad, en faradios.
es el área de las placas que se superponen, en metros cuadrados.
(épsilon) es la permitividad del material entre las placas. Es una medida de qué tan bien un material permite que se formen campos eléctricos.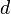
es la distancia de separación entre las placas, en metros.
Esta fórmula nos muestra que la capacidad es mayor si las placas son más grandes (mayor área) y si están más cerca una de la otra (menor distancia).
¿Cómo se mide la capacidad?
Medir la capacidad es importante no solo para saber cuánto puede almacenar un condensador, sino también para otras aplicaciones. Por ejemplo, algunos sensores de distancia funcionan midiendo cambios en la capacidad. Otros sensores que detectan presión, humedad o gases también pueden basarse en la medición de la capacidad.
Algunas formas de medir la capacidad son:
- Cargar el condensador con una corriente constante y observar qué tan rápido aumenta el voltaje.
- Usar un circuito resonante (un circuito que vibra a una frecuencia específica) y medir su frecuencia resonante.
- Aplicar un voltaje de corriente alterna (CA) y medir la corriente que fluye. Este método es muy común en los aparatos de medición de capacidad, ya que también pueden determinar otras propiedades del condensador.
Véase también
En inglés: Capacitance Facts for Kids
- Unidades de electromagnetismo del SI
