Campo gravitatorio para niños
En física, el campo gravitatorio o campo gravitacional es una forma de describir cómo la gravedad afecta el espacio alrededor de un objeto con masa. Imagina que tienes una pelota muy pesada. Si pones esa pelota en un lugar, el espacio a su alrededor cambia de una manera especial. Si luego acercas otra pelota más pequeña, sentirás que la primera pelota la atrae. Esa "influencia" que la pelota grande crea a su alrededor es lo que llamamos campo gravitatorio.
No podemos ver el campo gravitatorio directamente, solo notamos su efecto cuando otro objeto con masa entra en él. Es como el aire: no lo ves, pero sabes que está ahí cuando sientes el viento.
La forma en que los científicos entienden el campo gravitatorio ha cambiado con el tiempo:
- En la mecánica newtoniana (la física clásica), se ve como un campo vectorial, que es como un mapa donde cada punto tiene una flecha que indica la dirección y la fuerza de la gravedad.
- En la relatividad general de Einstein, el campo gravitatorio se entiende como una curvatura del espacio-tiempo mismo.
Contenido
El campo gravitatorio en la física clásica
En la física clásica, el campo gravitatorio se describe como un campo vectorial que siempre apunta hacia el centro del objeto que lo crea. Piensa en él como la fuerza que sentiría un objeto por cada kilogramo de su masa. Por eso, sus unidades son newtons por kilogramo (N/kg), que es lo mismo que una aceleración (metros por segundo al cuadrado, m/s²).
La intensidad del campo gravitatorio se calcula midiendo la fuerza que actúa sobre una "masa de prueba" (una masa muy pequeña) y dividiéndola por el valor de esa masa.
Una característica importante de los campos gravitatorios es que son aditivos. Esto significa que si tienes varias masas, el campo gravitatorio total en un punto es la suma de los campos creados por cada una de esas masas por separado.
¿Cómo se calcula la intensidad del campo gravitatorio?
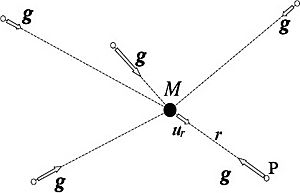
El campo gravitatorio creado por una masa puntual (como una estrella muy lejana) o por una esfera uniforme (como un planeta) en un punto fuera de ella, siempre apunta hacia el centro de esa masa. Su fuerza disminuye a medida que te alejas de la masa. Esta disminución sigue una regla llamada la ley de la inversa del cuadrado, lo que significa que si duplicas la distancia, la fuerza se reduce a una cuarta parte.
Por ejemplo, la intensidad del campo gravitatorio (g) creado por una masa (M) a una distancia (r) se calcula con la siguiente fórmula:
(1)Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{g}=-\frac{GM}{{{r}^{2}}}{{\mathbf{u}}_{r}}
Donde:
- G es la constante de la gravitación universal.
- M es la masa del objeto que crea el campo.
- r es la distancia desde el centro del objeto hasta el punto donde quieres calcular el campo.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u}_{r} es un vector que indica la dirección.
Esta fórmula es válida para puntos fuera de la esfera. Dentro de una esfera, el campo gravitatorio cambia de manera diferente, dependiendo de cómo se distribuye la masa.
Potencial gravitatorio: una forma de entender la energía
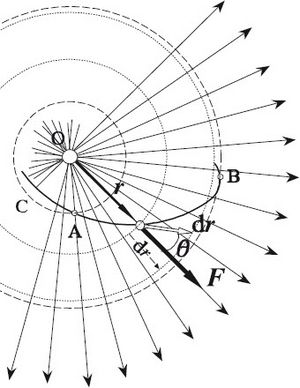
El campo gravitatorio es un "campo conservativo". Esto significa que el trabajo (la energía necesaria para mover un objeto) que realiza la gravedad entre dos puntos no depende del camino que sigas, solo de los puntos de inicio y fin.
Para entender esto mejor, los científicos usan el concepto de "potencial gravitatorio". Es una cantidad escalar (un número, no un vector) que se asigna a cada punto del espacio. Nos ayuda a saber cuánta energía potencial tiene un objeto en ese punto debido a la gravedad.
El potencial gravitatorio (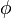 ) creado por una masa puntual o una esfera se calcula como:
) creado por una masa puntual o una esfera se calcula como:
Donde G y M son los mismos que antes, y r es la distancia. El signo negativo indica que el potencial disminuye a medida que te acercas a la masa.
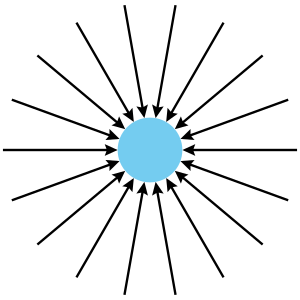
Líneas de campo: dibujando la gravedad
Las líneas de campo son una herramienta útil para visualizar un campo gravitatorio. Son líneas imaginarias que dibujamos para mostrar la dirección en la que actuaría la fuerza gravitatoria en cada punto. Las flechas en estas líneas indican la dirección de la fuerza. Cuanto más juntas estén las líneas, más fuerte es el campo en esa zona.
El campo gravitatorio en la física relativista
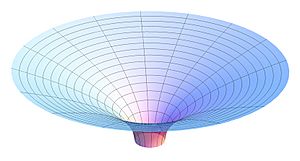
En la teoría de la relatividad general de Albert Einstein, el campo gravitatorio se entiende de una manera muy diferente. No se ve como una fuerza que atrae objetos, sino como una curvatura del espacio-tiempo.
Imagina que el espacio-tiempo es como una cama elástica gigante. Si pones una bola de boliche pesada en el centro, la cama elástica se curvará. Si luego lanzas una canica cerca de la bola de boliche, la canica no será "atraída" por la bola, sino que seguirá la curva de la cama elástica y rodará hacia la bola.
De manera similar, en la relatividad general, los objetos con masa (como planetas o estrellas) curvan el espacio-tiempo a su alrededor. Otros objetos, en lugar de ser atraídos por una fuerza, simplemente siguen las trayectorias más "rectas" posibles en este espacio-tiempo curvo. Estas trayectorias se llaman geodésicas. Así, lo que percibimos como gravedad es en realidad el efecto de los objetos moviéndose a través de un espacio-tiempo que ha sido curvado por la presencia de masa y energía.
Esta teoría es mucho más compleja que la física clásica y se usa para entender fenómenos a gran escala, como el movimiento de las galaxias o los agujeros negros.
Investiguese también
Bibliografía
- Fernández Rañada, Antonio (2005). Fondo de Cultura Económica, ed. Dinámica Clásico (1ª edición). México, D. F. pp. 302-304. ISBN 84-206-8133-4.
de:Gravitation#Gravitationsfeld
Véase también
 En inglés: Gravitational field Facts for Kids
En inglés: Gravitational field Facts for Kids