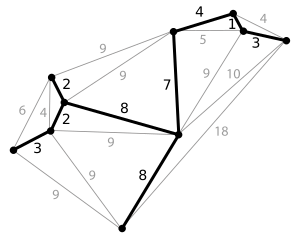
Árbol recubridor mínimo para niños
Un árbol recubridor mínimo (también conocido como árbol de expansión mínimo) es una forma especial de conectar todos los puntos de una red. Imagina que tienes varios lugares y quieres unirlos con caminos, pero usando la menor cantidad de material posible. Un árbol recubridor mínimo te ayuda a encontrar el plan más eficiente para conectar todos esos puntos sin crear bucles. Es como encontrar la manera más económica de unir todo.
Este concepto viene de la teoría de grafos, que es una parte de las matemáticas que estudia cómo se conectan los puntos (llamados vértices) y las líneas (llamadas aristas).
Contenido
Árbol Recubridor Mínimo: Conectando Puntos de la Mejor Manera
Para entender un árbol recubridor mínimo, primero necesitamos saber qué es un grafo. Un grafo es un conjunto de puntos (vértices) unidos por líneas (aristas). Si todas las aristas tienen un "peso" (un número que representa su costo, distancia o tiempo), podemos usar este peso para calcular el costo total de un camino.
¿Qué es un Árbol Recubridor?
Un árbol recubridor de un grafo es un subgrafo (una parte del grafo original) que cumple dos condiciones importantes:
- Debe ser un árbol: Esto significa que no tiene ningún ciclo (no hay caminos que empiecen y terminen en el mismo punto sin repetir aristas).
- Debe conectar todos los vértices del grafo original.
Piensa en una compañía de cable que necesita llevar internet a todas las casas de un nuevo barrio. Las casas son los vértices y los posibles caminos para tender el cable son las aristas. Un árbol recubridor sería un conjunto de esos caminos que conecte todas las casas sin crear bucles innecesarios.
¿Por qué es "Mínimo"?
Cada arista en el grafo tiene un "peso" asignado. Este peso puede representar el costo de instalar un cable, la distancia entre dos puntos o el tiempo que se tarda en ir de un lugar a otro. El peso total de un árbol recubridor se calcula sumando los pesos de todas sus aristas.
Un árbol recubridor mínimo es el árbol recubridor que tiene el menor peso total posible. Es decir, es la forma más barata o más corta de conectar todos los puntos sin crear bucles.
Puede haber más de un árbol recubridor mínimo si varias aristas tienen el mismo peso. Sin embargo, si todas las aristas tienen pesos diferentes, solo habrá un único árbol recubridor mínimo. En la vida real, es raro que dos caminos tengan exactamente el mismo costo, por lo que a menudo solo hay una solución óptima.
Si los pesos de las aristas son números positivos, el árbol recubridor mínimo es la forma más económica de conectar todos los vértices. Esto se debe a que cualquier subgrafo que contenga ciclos siempre tendrá un peso total mayor.
¿Para Qué Sirve un Árbol Recubridor Mínimo?
Los árboles recubridores mínimos tienen muchas aplicaciones prácticas. Una de las más importantes es en el diseño de redes. Por ejemplo:
- Redes de comunicación: Ayudan a diseñar redes eléctricas, telefónicas o de internet de la manera más eficiente. Los vértices serían los puntos de consumo (casas, oficinas) o los centros de distribución (centrales eléctricas, antenas), y las aristas serían los cables o las rutas de conexión.
- Transporte: Se usan para planificar rutas de transporte, como las rutas aéreas o las líneas de autobús, buscando la conexión más corta o económica entre diferentes ciudades o paradas.
- Diseño de circuitos: En electrónica, pueden ayudar a diseñar circuitos impresos para minimizar la longitud de los cables.
Cómo Encontrar un Árbol Recubridor Mínimo: El Algoritmo de Prim
Existen varios métodos para encontrar un árbol recubridor mínimo. Uno de los más conocidos es el Algoritmo de Prim. Este algoritmo construye el árbol paso a paso, añadiendo siempre la arista más "barata" que conecta un vértice ya incluido en el árbol con uno que aún no lo está.
Para usar el Algoritmo de Prim, el grafo debe estar conectado (es decir, debe ser posible ir de cualquier punto a cualquier otro) y todas sus aristas deben tener un peso.
Los pasos básicos del Algoritmo de Prim son:
- Se elige un vértice cualquiera del grafo para empezar. Este vértice será el primer elemento de nuestro árbol.
- Se busca la arista de menor peso que conecte un vértice que ya está en nuestro árbol con un vértice que aún no está.
- Se añade esa arista y el nuevo vértice a nuestro árbol.
- Se repiten los pasos 2 y 3 hasta que todos los vértices del grafo estén conectados en nuestro árbol.
Cuando el árbol tiene un número de aristas igual al número de vértices menos uno, significa que todos los vértices están conectados y el algoritmo ha terminado. El resultado será el árbol recubridor mínimo.
Véase también
 En inglés: Minimum spanning tree Facts for Kids
En inglés: Minimum spanning tree Facts for Kids
- Algoritmo de Prim
- Algoritmo de Kruskal
- Algoritmo de Dijkstra