Transformada de Fourier para niños
La transformada de Fourier es una herramienta matemática muy útil que nos ayuda a entender las señales. Imagina que tienes una canción: la transformada de Fourier puede separar esa canción en todas las notas y sonidos individuales que la componen. Es como si pudieras ver los "ingredientes" de una señal.
Esta herramienta fue nombrada en honor al matemático y físico francés Joseph Fourier (1768-1830).
La transformada de Fourier puede convertir una señal que cambia con el tiempo (como el sonido de una guitarra) en una señal que muestra qué frecuencias (o tonos) están presentes. También puede hacer lo contrario: convertir las frecuencias en una señal que cambia con el tiempo. Es reversible, ¡como un interruptor de encendido y apagado!
Cuando una señal se repite una y otra vez (como una nota musical sostenida), la transformada de Fourier se simplifica. En este caso, se usa algo llamado "series de Fourier" para encontrar las diferentes frecuencias que forman esa señal repetitiva.
La transformada de Fourier se usa en muchas áreas de la ciencia y la ingeniería, como la física, el procesamiento de señales (en electrónica), la óptica y el estudio de las propagación de ondas. En el procesamiento de señales, se usa para descomponer una señal en sus diferentes frecuencias.
La parte de las matemáticas que estudia la transformada de Fourier se llama análisis armónico.
Contenido
¿Qué es la Transformada de Fourier?
La transformada de Fourier nos muestra el "espectro de frecuencias" de una señal. Piensa en cómo funciona tu oído: recibe ondas de sonido y las descompone en diferentes frecuencias que luego escuchas. Sin embargo, tu oído percibe las frecuencias a medida que pasa el tiempo, mientras que la transformada de Fourier te da una vista completa de todas las frecuencias presentes en una señal, ¡como una foto de todos los sonidos a la vez!
¿Cómo se define la Transformada de Fourier?
Aunque las fórmulas matemáticas pueden ser complejas, la idea principal es que la transformada de Fourier toma una función (que representa una señal) y la convierte en otra función que nos dice qué tan fuerte es cada frecuencia en la señal original.
También existe una "transformada de Fourier inversa" que hace lo contrario: toma el espectro de frecuencias y lo convierte de nuevo en la señal original. La única diferencia entre ambas es un pequeño cambio en la fórmula, como un signo negativo.
Orígenes de la Transformada de Fourier
¿Quién la descubrió?
En 1821, Joseph Fourier propuso que cualquier función, incluso las que no son suaves o continuas, podía ser descompuesta en una serie de ondas simples (senos y cosenos). Este descubrimiento fue muy importante y otros científicos lo mejoraron, sentando las bases de las diferentes formas de la transformada de Fourier que usamos hoy.
¿Qué son las ondas complejas?
Cuando hablamos de las "ondas" que componen una señal, a menudo usamos números complejos en matemáticas. Estos números tienen una parte real y una parte imaginaria, y son muy útiles para describir tanto la fuerza (amplitud) como la posición inicial (fase) de cada onda de frecuencia.
¿Cómo se escribe la Transformada de Fourier?
La transformada de Fourier de una función se puede escribir de varias maneras, como:
- `mathcal{F}[f]`
- `hat{f}`
- `mathcal{F}(f(t))`
- `F(f)`
Características Principales
La transformada de Fourier tiene algunas propiedades importantes:
- Es lineal: Si sumas dos señales y luego aplicas la transformada, es lo mismo que aplicar la transformada a cada señal por separado y luego sumar los resultados.
- Cambio de escala: Si estiras o encoges una señal en el tiempo, su transformada de Fourier se encoge o estira de manera inversa en el dominio de la frecuencia.
- Desplazamiento: Si mueves una señal en el tiempo (la retrasas o adelantas), su transformada de Fourier cambia de una manera predecible.
- Derivadas: La transformada de Fourier puede simplificar el trabajo con derivadas de funciones, lo cual es muy útil en problemas de ingeniería y física.
Una operación importante relacionada es la convolución. Imagina que tienes dos señales y las "mezclas" de una manera especial. La transformada de Fourier de esa mezcla es simplemente el producto de las transformadas de Fourier de las señales originales. Esto simplifica mucho algunos cálculos.
¿Para qué se usa la Transformada de Fourier?
La transformada de Fourier es una herramienta muy poderosa en la ingeniería y la ciencia:
- Análisis de señales: Permite ver qué frecuencias son las más importantes en una señal. Por ejemplo, en una señal de radio, es más fácil saber en qué rango de frecuencias se concentra la energía si la analizamos con la transformada de Fourier.
- Diseño de filtros: Es fundamental para diseñar filtros que permiten pasar ciertas frecuencias y bloquear otras. Esto es crucial en radios, teléfonos y muchos otros dispositivos electrónicos.
- Procesamiento de imágenes: Se usa para mejorar o definir mejor ciertas partes de una imagen digital, como las fotos que ves en tu computadora o teléfono.
- Detección de materiales: Ayuda a identificar diferentes compuestos, materiales y aleaciones al analizar las frecuencias de ondas que transmiten.
Galería de imágenes
-
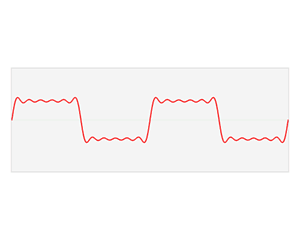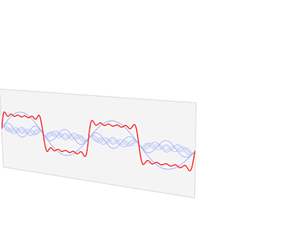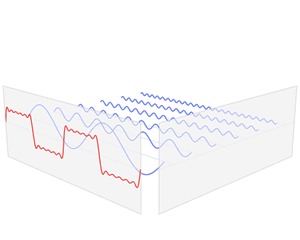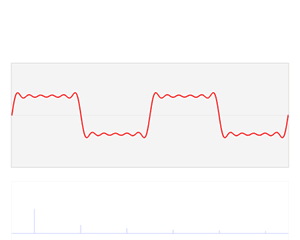
Un ejemplo de aplicación de la transformada de Fourier es determinar los tonos en una onda musical. Esta imagen muestra el resultado de aplicar una transformada a un acorde de piano. Los picos grandes corresponden a las notas principales (Do, Mi, Sol). Los picos más pequeños son sonidos adicionales de alta frecuencia.
Ver también
- Óptica de Fourier
- Transformada de Fourier discreta
- Transformada de Laplace
- Ondícula
Véase también
 En inglés: Fourier transform Facts for Kids
En inglés: Fourier transform Facts for Kids