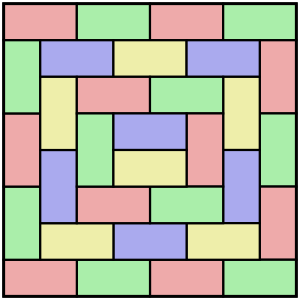
Teselado en dominó para niños
Un teselado en dominó es como un rompecabezas donde cubres una superficie con piezas llamadas "dominós". Imagina que tienes una forma hecha de muchos cuadrados pequeños, como un tablero de ajedrez. Un dominó es una pieza que une dos cuadrados iguales, uno al lado del otro. El objetivo es cubrir toda la forma sin dejar espacios y sin que las piezas se superpongan.
En matemáticas, esto se puede ver como un "pareado perfecto" en un tipo de dibujo llamado "grafo de celosía". Piensa que cada cuadrado de la forma es un punto (un "vértice") y si dos cuadrados están juntos, los conectas con una línea. Un teselado en dominó es cuando puedes emparejar todos los puntos con líneas sin que ninguna línea se cruce o comparta un punto.
Contenido
¿Cómo se usan las funciones de altura en los teselados?
Para entender mejor algunos teselados, especialmente en superficies planas, los matemáticos usan algo llamado "función de altura". Imagina que cada esquina de los cuadrados en tu tablero tiene un número. Empiezas con una esquina que tiene el número 0. Luego, a medida que te mueves de una esquina a otra, el número cambia.
Por ejemplo, en un tablero de ajedrez, si el cuadrado a la derecha de tu camino es negro, sumas uno al número de la esquina anterior. Si es blanco, restas uno. Así, cada esquina tiene una "altura" única. Esto ayuda a estudiar cómo se pueden organizar los dominós.
¿Qué es la condición de altura de Thurston?
El matemático William Thurston, en 1990, encontró una forma de saber si una forma hecha de cuadrados se puede cubrir con dominós. Él imaginó un mundo tridimensional donde cada punto tiene coordenadas (x, y, z).
La idea es que el borde de la forma que quieres cubrir se puede "levantar" y dibujar como un camino en este mundo tridimensional. Si este camino se cierra y forma una curva simple, es una señal de que la forma podría ser teselable. Thurston desarrolló un criterio más preciso que es muy útil para determinar si una región se puede cubrir con dominós.
¿Cómo se cuentan los teselados de una región?
Contar cuántas maneras diferentes hay de cubrir una forma con dominós es un desafío interesante. Por ejemplo, para un rectángulo de cierto tamaño, los matemáticos Temperley, Fisher y Kasteleyn encontraron una fórmula especial para calcular el número exacto de formas de cubrirlo.
Si el rectángulo tiene un lado impar, como 3x4, no se puede cubrir completamente con dominós, porque cada dominó cubre dos cuadrados y el área total sería impar. La fórmula lo muestra dando un resultado de cero.
Un caso curioso ocurre cuando intentas cubrir un rectángulo de 2xN (dos filas por N columnas). El número de formas de hacerlo sigue una secuencia muy famosa llamada la sucesión de Fibonacci. Esta secuencia empieza con 0 y 1, y cada número siguiente es la suma de los dos anteriores (0, 1, 1, 2, 3, 5, 8...).
Para cuadrados más grandes, como 2x2, 4x4, 6x6, etc., el número de soluciones aumenta muy rápido. Por ejemplo, un cuadrado de 8x8 tiene muchísimas formas de ser cubierto con dominós.
Un ejemplo visual de cómo el número de teselados puede cambiar mucho es el "diamante azteca". Un diamante azteca de orden 'n' tiene una cantidad enorme de teselados posibles. Pero si le haces pequeños cambios a su forma, el número de teselados puede disminuir drásticamente. Esto demuestra lo sensible que es el conteo de teselados a la forma de la región.
-
Un diamante azteca de orden 4, con 1024 posibles teselados en dominó
-
Uno de estos teselados
¿Qué son los tatamis?
Los tatamis son tapetes tradicionales japoneses que tienen forma de dominó (un rectángulo de 1x2). Se usan para cubrir el suelo de las habitaciones. Sin embargo, al colocarlos, hay reglas especiales.
Normalmente, se prefiere que solo tres tatamis se unan en una esquina. Si cuatro tatamis se juntan en una esquina, se considera una disposición no deseada. El problema de cubrir una habitación con tatamis siguiendo estas reglas puede ser bastante complicado de resolver.
Véase también
En inglés: Domino tiling Facts for Kids
- Física estadística
- Problema del tablero de ajedrez mutilado, un acertijo relacionado con el mosaico de dominó de un subconjunto de 62 casillas del tablero de ajedrez
