Soluciones óptimas para el cubo de Rubik para niños
Las soluciones óptimas para el cubo de Rubik se refieren a las formas más cortas de resolver este famoso rompecabezas. Hay dos maneras principales de medir qué tan corta es una solución:
- Contar cada giro de un cuarto de vuelta (90 grados). Esto se llama "métrica de cuarto de vuelta" (QTM).
- Contar cada giro de una cara exterior, sin importar si es un cuarto de vuelta o media vuelta (180 grados). Esto se llama "métrica de giro de cara" (FTM).
Por ejemplo, si giras una cara media vuelta, en QTM se cuentan dos movimientos, pero en FTM se cuenta solo uno.
El número mínimo de giros de cara necesarios para resolver cualquier cubo de Rubik es 20. Para la métrica de cuarto de vuelta, el número mínimo es 26. Estos números son como el "camino más corto" en un mapa gigante de todas las posibles posiciones del cubo. Un método que resuelve el cubo en el menor número de movimientos se conoce como un algoritmo de Dios.
Contenido
¿Cómo se escriben los movimientos del cubo de Rubik?
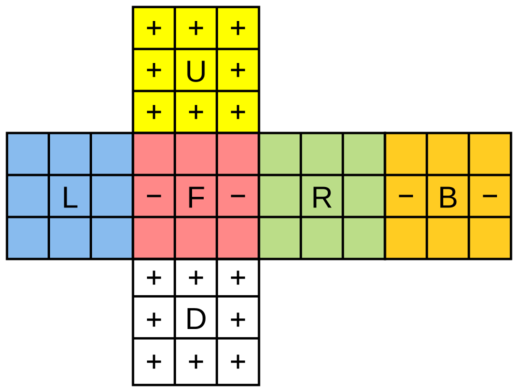
Para entender cómo se resuelven los cubos, es útil conocer la "notación Singmaster". Esta notación usa letras para representar los giros de las caras del cubo.
- L, R, F, B, U, D: Estas letras indican un giro de un cuarto de vuelta (90 grados) en el sentido de las agujas del reloj de las caras izquierda (Left), derecha (Right), frontal (Front), trasera (Back), superior (Up) e inferior (Down), respectivamente.
- 2: Si ves un número 2 después de una letra (por ejemplo, F2), significa que la cara se gira media vuelta (180 grados).
- ' (prima): Si ves un símbolo de prima (como R'), significa que la cara se gira un cuarto de vuelta en sentido contrario a las agujas del reloj.
También hay letras para girar las capas del medio:
- M: Gira la capa entre las caras R y L.
- S: Gira la capa entre las caras F y B.
- E: Gira la capa entre las caras U y D.
Estas también pueden llevar un 2 o una prima para indicar media vuelta o giro en sentido contrario.
Finalmente, las letras X, Y, Z (a menudo en minúscula) se usan para rotar todo el cubo:
- X: Gira el cubo hacia adelante 90 grados.
- Y: Gira el cubo hacia la izquierda 90 grados.
- Z: Gira el cubo en el sentido de las agujas del reloj 90 grados.
Estas rotaciones ayudan a que los algoritmos sean más fáciles de seguir.
¿Cuántos movimientos se necesitan como mínimo?
Los expertos han investigado mucho para saber cuál es el número mínimo de movimientos para resolver cualquier cubo de Rubik.
Descubriendo los límites inferiores
Se ha demostrado que existen posiciones del cubo que necesitan al menos 18 movimientos para resolverse. Esto se sabe comparando el número total de posiciones posibles del cubo con el número de posiciones que se pueden alcanzar con menos movimientos.
Una posición muy difícil de resolver es el "superflip". En esta posición, todas las esquinas están bien, pero todas las piezas de los bordes están giradas incorrectamente. En 1992, se encontró una solución para el superflip con 20 giros de cara. Más tarde, en 1995, se demostró que esta era la cantidad mínima de movimientos para esa posición. También en 1995, se encontró una solución para el superflip en 24 cuartos de vuelta. En 1998, se descubrió una posición aún más difícil, llamada "superflip compuesto con cuatro puntos", que necesita 26 cuartos de vuelta para resolverse.
¿Cuántos movimientos se necesitan como máximo?
Al principio, los algoritmos que usaban las personas para resolver el cubo podían necesitar hasta 100 movimientos.
Primeros avances en los límites superiores
A principios de 1979, David Singmaster mencionó que su algoritmo podía resolver el cubo en un máximo de 277 movimientos. Poco después, otros expertos idearon un algoritmo que requería un máximo de 160 movimientos. Más tarde, se logró reducir este número a 94 movimientos.
El algoritmo de Thistlethwaite
Un gran avance fue el algoritmo de Morwen Thistlethwaite, publicado en 1981. Su idea fue dividir el problema de resolver el cubo en pasos más pequeños. En lugar de intentar resolver todo el cubo de una vez, lo dividió en etapas, donde en cada etapa se permitían ciertos tipos de movimientos.
Aunque el número total de posiciones del cubo es enorme (alrededor de 43 trillones), el algoritmo de Thistlethwaite dividió el problema en partes más manejables. Inicialmente, Thistlethwaite demostró que cualquier configuración podía resolverse en un máximo de 85 movimientos. Luego, mejoró su estrategia, reduciendo el máximo a 80, luego a 63, y finalmente a 52 movimientos. Con más investigación, se encontró que el peor caso para cada etapa de su algoritmo sumaba un total de 45 movimientos como máximo.
El algoritmo de Kociemba
En 1992, Herbert Kociemba mejoró el algoritmo de Thistlethwaite. Simplificó el proceso usando solo dos grupos intermedios en lugar de varios. Este algoritmo busca primero llevar el cubo a un estado intermedio y luego encontrar la solución óptima desde ese estado.
Con este algoritmo, las soluciones suelen encontrarse en menos de 21 movimientos. En 1995, Michael Reid demostró que, usando estos dos grupos, cualquier posición se puede resolver en un máximo de 29 giros de cara o 42 cuartos de vuelta. Este resultado fue mejorado a 40 cuartos de vuelta en 2005.
El algoritmo de Korf
En 1997, Richard Korf presentó un algoritmo que podía resolver cubos de forma óptima (en el menor número de movimientos). Su método se llama IDA* y se basa en dividir el problema en partes más pequeñas.
Korf identificó subproblemas que son lo suficientemente pequeños como para resolverse de forma óptima, como:
- Resolver solo las esquinas del cubo, sin mirar los bordes.
- Resolver solo 6 bordes, sin mirar las esquinas ni los otros bordes.
- Resolver los otros 6 bordes.
El número de movimientos necesarios para resolver cualquiera de estos subproblemas es un límite mínimo para el número de movimientos necesarios para resolver todo el cubo. Este algoritmo siempre encuentra soluciones óptimas.
Más mejoras y el "Número de Dios"
Los investigadores continuaron trabajando para encontrar el número exacto de movimientos necesarios para resolver cualquier cubo.
- En 2006, Silviu Radu demostró que cualquier posición se puede resolver en un máximo de 27 giros de cara o 35 cuartos de vuelta.
- En 2007, Daniel Kunkle y Gene Cooperman usaron una supercomputadora para mostrar que todos los cubos se pueden resolver en no más de 26 movimientos (en métrica de giro de caras).
- En 2008, Tomas Rokicki informó que todos los cubos se podían resolver en 25 movimientos o menos, luego lo redujo a 23, y finalmente a 22 movimientos.
Finalmente, en 2010, Tomas Rokicki, Herbert Kociemba, Morley Davidson y John Dethridge, con la ayuda de computadoras, demostraron que todas las posiciones del cubo se pueden resolver con un máximo de 20 giros de caras. Este número es conocido como el "Número de Dios" para la métrica de giro de caras.
Para la métrica de cuarto de vuelta, en 2009, Tomas Rokicki demostró que 29 movimientos son suficientes. Y en 2014, Tomas Rokicki y Morley Davidson demostraron que el número máximo de cuartos de vuelta necesarios para resolver el cubo es 26.
Es interesante que, aunque hay cientos de millones de posiciones que necesitan 20 giros de cara para resolverse, solo se conoce una posición (y sus rotaciones) que necesita el máximo de 26 cuartos de vuelta.
Galería de imágenes