Significación estadística para niños

En estadística, decimos que un resultado o efecto es estadísticamente significativo cuando es muy poco probable que haya ocurrido solo por azar. Esto significa que tenemos pruebas matemáticas de que hay una diferencia o un efecto real, y no que la diferencia sea enorme o súper importante.

El nivel de significación es un concepto clave en estadística. Imagina que estás probando una idea (llamada hipótesis). El nivel de significación es la probabilidad de que te equivoques al decir que tu idea es correcta, cuando en realidad no lo es. A este error se le llama error de tipo I o falso positivo.

Para decidir si un resultado es significativo, se usa algo llamado valor p. Si el valor p es más pequeño que el nivel de significación que elegiste, entonces se considera que tu resultado es significativo. Cuanto más pequeño sea el valor p, más fuerte es la evidencia de que tu resultado no fue por casualidad.

¿Cómo se usa en la práctica?

El nivel de significación se representa con la letra griega α (alfa). Los niveles más comunes que se usan son 0.05, 0.01 y 0.001.

¿Qué significa el nivel alfa (α)?

Si el valor p de tu estudio es menor que el nivel α que elegiste, entonces tu resultado se considera estadísticamente significativo. Esto quiere decir que hay una buena razón para creer que lo que observaste no fue solo suerte o coincidencia. Cuanto más bajo sea el valor de α, más fuerte será la prueba de que un evento no ocurrió por simple casualidad.

A veces, es útil pensar en la significación como 1 - α. Por ejemplo, si α es 0.05, entonces 1 - α es 0.95, lo que significa que hay un 95% de confianza en que el resultado no es por azar.

Elegir el nivel de significación

Elegir un nivel de α tiene sus ventajas y desventajas. Si eliges un α muy pequeño (por ejemplo, 0.001), estás muy seguro de que, si encuentras un resultado significativo, no es por casualidad. Pero, al mismo tiempo, corres un riesgo mayor de no encontrar un efecto real que sí existe. A esto se le llama error de tipo II o falso negativo.

Por eso, al elegir el nivel de α, hay que buscar un equilibrio entre la seguridad de no equivocarse al decir que algo es significativo y la posibilidad de encontrar un efecto real.

Significación en la ciencia

En algunos campos de la ciencia, como la física, es común expresar la significación estadística usando unidades de σ (sigma), que es el desvío estándar de una distribución de Gauss. Por ejemplo, si un resultado se desvía 3σ de lo esperado, significa que la probabilidad de que eso ocurriera por casualidad es muy baja, aproximadamente 0.27%.

Aunque los niveles fijos de significación son útiles, la estadística moderna recomienda que, al final de un experimento o estudio, se mencione el valor p exacto. Esto permite que otros investigadores puedan entender mejor los resultados y usarlos en estudios más grandes.

Galería de imágenes

• 

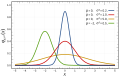
  Una distribución normal o de Gauss, importante en estadística.

Véase también

En inglés: Statistical significance Facts for Kids