Serie divergente para niños
Una serie divergente es un tipo especial de lista de números que se suman, pero que no tienen un resultado final fijo. Imagina que tienes una lista infinita de números que quieres sumar. Si el resultado de esa suma se acerca cada vez más a un número específico, decimos que la serie es convergente. Pero si el resultado sigue creciendo sin parar, o salta de un lado a otro sin acercarse a un solo número, entonces la serie es divergente.
Para que una serie sea convergente, los números individuales que se están sumando deben volverse cada vez más pequeños, acercándose a cero. Si los números no se hacen más pequeños y no se acercan a cero, entonces la serie definitivamente será divergente.
Sin embargo, que los números se acerquen a cero no siempre significa que la serie convergerá. Un ejemplo famoso de esto es la serie armónica: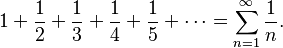 
En esta serie, cada número es más pequeño que el anterior (1, luego 0.5, luego 0.333...). Aunque los términos se hacen muy pequeños, la suma total de la serie armónica sigue creciendo sin límite, lo que la convierte en una serie divergente. Un matemático de la Edad Media llamado Nicole Oresme demostró que esta serie es divergente.
A veces, los matemáticos pueden usar métodos especiales, llamados métodos de sumación, para asignar un valor a algunas series divergentes. Por ejemplo, la sumación de Cesàro puede asignar el valor de 1/2 a la serie de Grandi, que es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 - 1 + 1 - 1 + \cdots Esta serie salta entre 0 y 1 si la sumas de forma normal, pero con el método de Cesàro, se le puede dar un valor.
Contenido
¿Cómo funcionan los métodos de sumación?
Para que un método de sumación sea útil, debe cumplir con ciertas reglas:
Propiedades importantes
- Regularidad: Si una serie ya es convergente y tiene un resultado, el método de sumación debe dar el mismo resultado. No debe cambiar lo que ya se sabe.
- Linealidad: Si combinas series (sumándolas o multiplicándolas por un número), el método de sumación debe funcionar de manera lógica con esas combinaciones.
- Estabilidad: Si quitas el primer número de una serie, el resultado de la sumación debe cambiar de una manera predecible.
También es importante que los diferentes métodos de sumación sean consistentes entre sí. Esto significa que si dos métodos pueden darle un valor a la misma serie, ambos métodos deben dar el mismo valor. Si un método puede sumar más series que otro, se dice que es más potente.
Es interesante saber que existen algunos métodos de sumación muy poderosos que no cumplen con todas estas propiedades, como las transformaciones de series no lineales.
Promedio Abeliano
El promedio abeliano es un tipo de método de sumación que se usa para series infinitas. Imagina que tienes una serie de números y creas una función especial con ellos. Si esa función se acerca a un valor específico cuando una variable se acerca a cero, ese valor se considera el promedio abeliano de la serie.
Los promedios abelianos suelen ser regulares, lineales y estables. Sin embargo, no siempre son consistentes entre sí.
Sumación de Abel
Un caso especial del promedio abeliano es la sumación de Abel. En este método, se usa una serie de potencias (una suma de términos con potencias crecientes de una variable) para encontrar el valor de una serie divergente. La sumación de Abel es muy útil porque es consistente con la sumación de Cesàro y, de hecho, es más potente, lo que significa que puede sumar más series que la sumación de Cesàro.
Véase también
En inglés: Divergent series Facts for Kids
- 1 + 2 + 3 + 4 + ⋯
- Test de divergencia
