Rompecabezas MU para niños

Enciclopedia para niños

El rompecabezas MU es un rompecabezas formulado por Douglas Hofstadter y encontrado en Gödel, Escher, Bach que involucra un sistema formal simple llamado "MIU". La motivación de Hofstadter es contrastar el razonamiento dentro de un sistema formal (es decir, derivar teoremas) contra el razonamiento sobre el sistema formal en sí. MIU es un ejemplo de un sistema post canónico y puede reformularse como un sistema de reescritura de cadenas.

Contenido

El rompecabezas
Solución
- Un criterio decidible para la derivabilidad
- Prueba
  - Ejemplo
Aritmetización
Véase también

El rompecabezas

Supongamos que existen los símbolos M, I, y U que se pueden combinar para producir cadenas de símbolos. El rompecabezas MU le pide a uno que comience con la cadena "axiomática" MI y la transformes en la cadena MU usando en cada paso una de las siguientes reglas de transformación:

Aquí:caracter I.

Nr.	Regla formal			Explicación informal	Ejemplo
1.	x`I`	→	x`IU`	Agregue la `U` al final de cualquier cadena que termine en `I`	`MI`	a	`MIU`
2.	`M`x	→	`M`xx	Duplica la secuencia después de `M`	`MIU`	a	`MIUIU`
3.	x`III`y	→	x`U`y	Reemplaza cualquier `III` con una `U`	`MUIIIU`	a	`MUUU`
4.	x`UU`y	→	xy	Elimina cualquier `UU`	`MUUU`	a	`MU`

Solución

El rompecabezas no se puede resolver: es imposible cambiar la cadena MI a MU aplicando repetidamente las reglas dadas. En otras palabras, MU no es un teorema del sistema formal MIU. Para probar esto, uno debe salir "fuera" del sistema formal en sí. Para probar afirmaciones como esta, a menudo es beneficioso buscar una invariante ; es decir, alguna propiedad que no cambia mientras se aplican las reglas. En este caso, se puede ver el número total de I en una cadena. Solo las reglas segunda y tercera cambian este número. En particular, la regla dos lo duplicará mientras que la regla tres lo reducirá en 3.Ahora, la propiedad invariable es que el número de I's no es divisible por 3:

Al principio, el número de I's es 1, que no es divisible por 3.
Duplicar un número que no es divisible por 3 no lo hace divisible por 3.
Restar 3 de un número que no es divisible por 3 tampoco lo hace divisible por 3.

Por lo tanto, el objetivo de MU con cero I no se puede lograr porque 0 es divisible por 3.

En el lenguaje de la aritmética modular , el número n de I obedece a la congruencia

n \equiv 2^a \not\equiv 0 \pmod 3.\,

donde a cuenta con qué frecuencia se aplica la segunda regla.

Un criterio decidible para la derivabilidad

En términos más generales, las cuatro reglas anteriores pueden derivar una cadena x dada de manera arbitraria si, y solo si , x respeta las tres propiedades siguientes:

x solo se compone de una M y cualquier cantidad de I y U,
x comienza con M, y
el número de I en x no es divisible por 3.

Prueba

Sólo si: No hay ninguna regla que mueva la M, cambie el número de M, o introduzca cualquier carácter de M,I,U. Por lo tanto, cada x deriva de MI respecto a las propiedades 1 y 2. Como se mostró anteriormente, también respeta la propiedad 3.

Si: Si x respeta las propiedades de la 1 a la 3,deja a $N_{I}$ y $N_{U}$ ser el número de I y U en x, respectivamente, y deja a $N = N_{I} + 3N_{U}$ .Por la propiedad 3, el número de $N_{I}$ no puede ser divisible por 3, por lo tanto, $N$ tampoco lo puede ser. Es decir, $N \equiv 1 \text{ or } N \equiv 2 \pmod 3$ . $n \in \N$ such that $2^n > N$ and $2^n \equiv N \pmod 3$ . Comenzando desde el axioma MI, aplicando la segunda regla $n$ veces, se obtiene MIII...I con $2^n$ I.Ya que $2^n - N$ es divisible por 3, por la interpretación de $n$ , aplicando la tercera regla $\frac{2^n - N}{3}$ se obtendrán MIII...IU...U, con exactamente $N$ I, seguidos de algún número de U. El recuento de U siempre se puede hacer de manera uniforme, aplicando la primera regla si es necesario. Aplicando la cuarta regla con la suficiente frecuencia, todo U se puede eliminar, obteniendo así MIII...I with $N_{I} + 3N_{U}$ I.Aplicando la tercera regla para reducir las triples I a U en los lugares correctos obtendrá x. x se ha derivado de MI.

Ejemplo

Para ilustrar la interpretación del Si, la cadena MIIUII, que respeta las propiedades de la 1 a la 3, conduce a $N_I=4$ , $N_U=1$ , $N=7$ , $n=4$ ; por tanto, puede derivarse de la siguiente manera:

MI

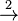
\stackrel{2}{\to}

MII

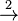
\stackrel{2}{\to}

MIIII

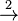
\stackrel{2}{\to}

MIIIIIIII

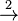
\stackrel{2}{\to}

MIIIIIIIIIIIIIIII

\stackrel{3}{\to}

MIIIIIIIUIIIIII

\stackrel{3}{\to}

MIIIIIIIUUIII

\stackrel{3}{\to}

MIIIIIIIUUU

\stackrel{1}{\to}

MIIIIIIIUUUU

\stackrel{4}{\to}

MIIIIIIIUU

\stackrel{4}{\to}

MIIIIIII

\stackrel{3}{\to}

MIIUII.

Aritmetización

El Capítulo XIX de Gödel, Escher, Bach ofrece un plano del sistema MIU a la aritmética, de la siguiente manera: En primer lugar, cada secuencia MIU se puede traducir a un número entero mediante la asignación de las letras M, I, y U a los números 3,1 y 0, respectivamente. (Por ejemplo, la cadena MIUIU se asignaría a 31010.) En segundo lugar, el axioma único del sistema MIU, es decir, la cadena MI, se convierte en el número 31 Tercero, las cuatro reglas dadas arriba se convierten en las siguientes

Nr.	Regla formal			Ejemplo
1.	k × 10 + 1	→	10 × (k × 10 + 1)	31	→	310	(k = 3)
2.	3 × 10^m + n	→	10^m × (3 × 10^m + n) + n	310	→	31010	(m = 2, n = 10)
3.	k × 10^{m + 3} + 111 × 10^m + n	→	k × 10^{m + 1} + n	3111011	→	30011	(k = 3, m = 3, n = 11)
4.	k × 10^{m + 2} + n	→	k × 10^m + n	30011	→	311	(k = 3, m = 2, n = 11)

(NB: La representación de las reglas anteriores concretamente la primera, difiere superficialmente de la del libro,donde está escrita como "[i]f hemos hecho 10m + 1, entonces podemos hacer 10 × (10m + 1)". Aquí, sin embargo, la variable m estaba reservada para su uso solamente en exponentes de 10 , y por lo tanto, se reemplazo por k en la primera regla. Además, en esta representación, la disposición de los factores en esta regla se hizo consistente con la de las otras tres.)

Véase también

En inglés: MU puzzle Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Rompecabezas_MU&oldid=3841870»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Rompecabezas MU para Niños. Enciclopedia Kiddle.