Prueba χ² para niños
La prueba χ² (se pronuncia "ji al cuadrado" o "chi al cuadrado") es una herramienta muy útil en estadística. Imagina que quieres saber si algo que observas en la vida real (como los resultados de un experimento) se parece a lo que esperarías si una idea inicial fuera cierta. Esta prueba te ayuda a decidir si las diferencias entre lo que ves y lo que esperas son solo por casualidad o si son lo suficientemente grandes como para decir que tu idea inicial no es correcta.
Se usa mucho para comparar grupos de datos. Por ejemplo, si quieres saber si la cantidad de veces que sale cada número en un dado es la que esperarías (es decir, si el dado está equilibrado), o si hay una relación entre dos cosas, como el tipo de trabajo de una persona y el barrio donde vive.
La prueba χ² funciona calculando un número especial. Si este número es muy grande, significa que lo que observaste es muy diferente de lo que esperabas, y entonces puedes pensar que tu idea inicial (llamada "hipótesis nula") probablemente no es cierta. Si el número es pequeño, significa que las diferencias son normales y podrían ser solo por casualidad.
Contenido
Historia de la Prueba Chi-cuadrado
¿Quién inventó la Prueba Chi-cuadrado?
A finales del siglo XIX, los científicos usaban mucho las matemáticas para entender la biología. Muchos pensaban que los datos que recogían siempre seguían un patrón llamado "distribución normal", que es como una campana.
Pero un matemático llamado Karl Pearson se dio cuenta de que no siempre era así. A veces, los datos tenían una forma diferente, no tan simétrica. Para poder estudiar estos datos de forma más precisa, Pearson desarrolló nuevas formas de entender cómo se distribuyen los números.
En el año 1900, Karl Pearson publicó un trabajo muy importante sobre la prueba χ². Este trabajo es considerado uno de los pilares de la estadística moderna. Con esta prueba, Pearson dio una forma de saber si los datos que observamos se ajustan bien a un modelo o a una idea que tenemos.
¿Cómo funciona la Prueba Chi-cuadrado?
La prueba χ² se usa para comparar las "frecuencias observadas" (lo que realmente pasó en tu experimento) con las "frecuencias esperadas" (lo que crees que debería pasar si tu idea inicial fuera cierta).
Por ejemplo, si lanzas una moneda 100 veces, esperarías que saliera cara 50 veces y cruz 50 veces. Esas son tus frecuencias esperadas. Si al lanzarla obtienes 45 caras y 55 cruces, esas son tus frecuencias observadas. La prueba χ² te ayuda a ver si esa diferencia (50 vs 45, y 50 vs 55) es lo suficientemente grande como para decir que la moneda no está equilibrada, o si es una diferencia normal que puede pasar por casualidad.
Para hacer esto, la prueba calcula un valor que mide qué tan grandes son las diferencias entre lo observado y lo esperado. Cuanto mayor sea este valor, más probable es que haya una diferencia real y no solo una casualidad.
Ejemplo: ¿Está un dado equilibrado?
Imagina que quieres saber si un dado de seis caras está bien equilibrado. Si lo está, esperarías que cada número (del 1 al 6) saliera la misma cantidad de veces.
Paso 1: La idea inicial (Hipótesis Nula)
Tu idea inicial, o "hipótesis nula", es: "El dado está equilibrado".
Paso 2: El experimento
Lanzas el dado 600 veces. Si el dado estuviera perfectamente equilibrado, esperarías que cada número saliera 100 veces (600 lanzamientos / 6 caras = 100 veces por cara). Estas son tus frecuencias esperadas.
Ahora, anotas los resultados reales de tus 600 lanzamientos. Estas son tus frecuencias observadas:
| Número que sale | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Veces que salió | 88 | 109 | 107 | 94 | 105 | 97 |
Paso 3: Calcular el valor Chi-cuadrado
La prueba χ² compara cada frecuencia observada con su frecuencia esperada. Se calcula una suma de las diferencias al cuadrado, divididas por la frecuencia esperada.
Para el primer resultado (88 veces el 1, cuando esperabas 100): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{(88-100)^2}{100} = \frac{(-12)^2}{100} = \frac{144}{100} = 1.44
Haces esto para cada número y luego sumas todos los resultados. En nuestro ejemplo, el valor total de la prueba χ² es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{(88-100)^2}{100}+\frac{(109-100)^2}{100}+\frac{(107-100)^2}{100}+\frac{(94-100)^2}{100}+\frac{(105-100)^2}{100}+\frac{(97-100)^2}{100} = 3.44
Paso 4: Interpretar el resultado
Para saber si 3.44 es un valor grande o pequeño, lo comparamos con un valor de una tabla especial (la tabla de la distribución χ²). Esta tabla nos dice qué valor esperaríamos si el dado estuviera realmente equilibrado. También necesitamos saber los "grados de libertad", que es el número de categorías menos 1. En este caso, 6 caras - 1 = 5 grados de libertad.
Si el valor calculado (3.44) es menor que el valor de la tabla (que para 5 grados de libertad y un riesgo del 5% es 11.07), significa que las diferencias que observamos son normales y podrían ser solo por casualidad. En este caso, no podemos decir que el dado esté amañado.
¿Qué pasaría si los resultados fueran diferentes? Supongamos que los resultados del experimento fueran:
| Número que sale | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Veces que salió | 89 | 131 | 93 | 92 | 104 | 91 |
Calculando el valor χ² con estos nuevos datos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{(89-100)^2}{100}+\frac{(131-100)^2}{100}+\frac{(93-100)^2}{100}+\frac{(92-100)^2}{100}+\frac{(104-100)^2}{100}+\frac{(91-100)^2}{100} = 12.92
Ahora, el valor calculado es 12.92. Como 12.92 es mayor que 11.07 (el valor de la tabla), podemos decir que las diferencias son demasiado grandes para ser solo casualidad. En este caso, la prueba χ² nos permite pensar que el dado sí está amañado.
Ejemplo: ¿Hay relación entre el barrio y el tipo de trabajo?
Imagina que en una ciudad con cuatro barrios (A, B, C, D), quieres saber si el barrio donde vive una persona tiene alguna relación con su tipo de trabajo (trabajador de "cuello blanco", "cuello azul" o "sin cuello").
Paso 1: La idea inicial (Hipótesis Nula)
Tu hipótesis nula es: "El barrio de residencia de una persona es independiente de su tipo de trabajo". Es decir, no hay relación entre ellos.
Paso 2: Recoger datos
Tomas una muestra de 650 personas y anotas su barrio y su tipo de trabajo:
| A | B | C | D | Total | |
|---|---|---|---|---|---|
| Cuello blanco | 90 | 60 | 104 | 95 | 349 |
| Cuello azul | 30 | 50 | 51 | 20 | 151 |
| Ni cuello blanco ni azul | 30 | 40 | 45 | 35 | 150 |
| Total | 150 | 150 | 200 | 150 | 650 |
Paso 3: Calcular las frecuencias esperadas
Si no hubiera relación (si la hipótesis nula fuera cierta), ¿cuántos trabajadores de cuello blanco esperaríamos en el barrio A? Calculamos la proporción de trabajadores de cuello blanco en toda la muestra (349 de 650) y la multiplicamos por el total de personas en el barrio A (150). Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 150 \times \frac{349}{650} \approx 80.54 Así, esperaríamos unos 80.54 trabajadores de cuello blanco en el barrio A si no hubiera relación. Pero observamos 90.
Paso 4: Calcular el valor Chi-cuadrado
Para cada "casilla" de la tabla, calculamos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\left(\text{observado}-\text{esperado}\right)^2}{\text{esperado}} Para la casilla de "cuello blanco" en el barrio A: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\left(90-80.54\right)^2}{80.54} \approx 1.11
Hacemos esto para todas las casillas y sumamos los resultados. En este ejemplo, la suma total es aproximadamente 24.57.
Paso 5: Interpretar el resultado
Para interpretar este valor, necesitamos los grados de libertad. Se calculan como (número de filas - 1) * (número de columnas - 1). En este caso, (3-1) * (4-1) = 2 * 3 = 6 grados de libertad.
Si el valor calculado (24.57) es muy grande comparado con el valor de la tabla para 6 grados de libertad, entonces podemos decir que hay una relación significativa entre el barrio y el tipo de trabajo. Un valor de 24.57 es bastante grande, lo que nos haría pensar que sí hay una relación.
Aplicaciones de la Prueba Chi-cuadrado
La prueba χ² se usa en muchos campos:
- Criptografía: Ayuda a los expertos a descifrar códigos secretos. Comparan cómo se distribuyen las letras en un mensaje cifrado con cómo se distribuyen en un idioma normal. Si el descifrado es correcto, las distribuciones deberían parecerse.
- Bioinformática: Se usa para comparar características de los genes, como su tamaño o cómo se agrupan, en diferentes tipos de genes (por ejemplo, genes relacionados con enfermedades frente a genes normales).
- Investigación de mercados: Para ver si hay relación entre el gusto por un producto y la edad de las personas, o su lugar de residencia.
- Ciencias sociales: Para estudiar si hay relación entre la opinión de las personas sobre un tema y su nivel educativo o su género.
Galería de imágenes
-
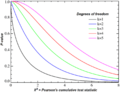
Distribución χ², mostrando χ2 en el eje x y el valor p (probabilidad de cola derecha) en el eje y
Véase también
 En inglés: Chi-squared test Facts for Kids
En inglés: Chi-squared test Facts for Kids