Problema del trigo y del tablero de ajedrez para niños
El problema del trigo y el tablero de ajedrez es un famoso desafío matemático. También se le conoce a veces usando granos de arroz en lugar de trigo. La pregunta es la siguiente:
Imagina que colocas un grano de trigo en la primera casilla de un tablero de ajedrez. Luego, pones dos granos en la segunda casilla, cuatro en la tercera, y así sucesivamente, duplicando la cantidad de granos en cada casilla. ¿Cuántos granos de trigo habría en total en el tablero al final?
Contenido
¿Qué es el problema del trigo y el tablero de ajedrez?
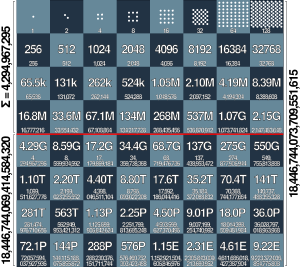
Este problema nos ayuda a entender cómo funciona el crecimiento exponencial, que es cuando algo aumenta muy rápido. En un tablero de ajedrez hay 64 casillas. Si empezamos con 1 grano y lo duplicamos en cada casilla, la cantidad crece de forma asombrosa.
¿Cuántos granos de trigo hay en total?
La cantidad de granos en cada casilla se puede escribir usando potencias de 2:
- Casilla 1: 1 grano (que es 2 elevado a la potencia 0, o 20)
- Casilla 2: 2 granos (21)
- Casilla 3: 4 granos (22)
- Y así hasta la última casilla, la número 64, que tendría 263 granos.
Solo en la última casilla, la número 64, habría una cantidad enorme de granos: 9,223,372,036,854,775,808. ¡Es un número gigantesco!
Si sumamos todos los granos de las 64 casillas, el total es: 18,446,744,073,709,551,615 granos de trigo.
Este número es mucho más grande de lo que la mayoría de la gente esperaría al principio. Es una excelente manera de ver lo rápido que crecen las series exponenciales y las series geométricas.
¿Cómo se calcula esta cantidad?
Aunque la suma parece muy larga, hay una forma sencilla de calcularla. La suma de una serie donde cada número es el doble del anterior (como 1 + 2 + 4 + ... + 263) es igual a 2 elevado a la potencia del número total de casillas, menos 1.
En este caso, como hay 64 casillas, la suma total es 264 - 1. Esto nos da el número final: 18,446,744,073,709,551,615.
¿Cuánto trigo es en la vida real?
Para entender mejor esta cantidad, podemos hacer una estimación. Si un kilogramo de trigo tiene aproximadamente 20,000 granos, entonces el total de granos del problema equivaldría a:
- 922,337,203,685,477 kilogramos de trigo.
- O lo que es lo mismo, 922,337,203,685 toneladas métricas.
Para ponerlo en perspectiva, la producción mundial de trigo en un año (por ejemplo, en 2017) fue de unos 771,718,579 toneladas métricas. Esto significa que para juntar la cantidad de trigo del tablero, ¡se necesitarían las cosechas mundiales de trigo de aproximadamente 1,195 años!
Origen e historia del problema
La historia de este problema está ligada a la invención del ajedrez. Aunque hay varias versiones, todas cuentan una historia similar:
Un sabio matemático (o inventor) de la India creó el juego del ajedrez y se lo presentó a un rey. El rey quedó tan impresionado que le ofreció al inventor cualquier recompensa que deseara. El sabio, que era muy inteligente, pidió algo que parecía muy humilde: un grano de trigo por la primera casilla, dos por la segunda, cuatro por la tercera, y así sucesivamente, duplicando la cantidad en cada casilla.
El rey, que no era muy bueno con los números, aceptó rápidamente, pensando que era una petición muy pequeña. Incluso se sintió un poco ofendido por lo poco que pedía el inventor. Ordenó a su tesorero que contara los granos y se los entregara.
Sin embargo, el tesorero tardó más de una semana en hacer los cálculos. Cuando el rey le preguntó por la tardanza, el tesorero le explicó que la cantidad de granos era tan inmensa que superaba todas las riquezas del reino. En algunas versiones de la historia, el inventor se convierte en el nuevo rey, mientras que en otras, el rey, al darse cuenta del engaño, castiga al inventor.
Aplicaciones educativas del problema
Este problema es una excelente herramienta para aprender sobre varios conceptos matemáticos importantes:
- Exponentes y potencias: Cómo un número se multiplica por sí mismo varias veces (como 20, 21, 22, etc.).
- Sumatorias: Una forma de escribir sumas muy largas de manera sencilla usando el símbolo de sigma (Σ).
- Series geométricas: Son secuencias de números donde cada término se obtiene multiplicando el anterior por una cantidad fija (en este caso, por 2).
- Crecimiento exponencial: Demuestra lo increíblemente rápido que pueden crecer las cantidades cuando se duplican repetidamente.
La segunda mitad del tablero
Existe una frase, "la segunda mitad del tablero de ajedrez", que se usa para describir el punto en el que el crecimiento exponencial se vuelve tan grande que tiene un impacto enorme.
Aunque la primera mitad del tablero (las primeras 32 casillas) ya acumula una cantidad considerable de granos, la cantidad en la segunda mitad (las casillas 33 a la 64) es muchísimo mayor. De hecho, la cantidad de granos en la segunda mitad es miles de millones de veces más grande que la de la primera mitad.
- En la primera mitad del tablero (casillas 1 a 32), el total de granos es 4,294,967,295.
- Solo la casilla número 33 (la primera de la segunda mitad) contiene más granos que todas las 32 casillas anteriores juntas.
- La cantidad total de granos en la segunda mitad es 264 - 232.
Este concepto nos enseña que, en el crecimiento exponencial, los cambios más grandes y significativos a menudo ocurren en las etapas finales.
Galería de imágenes
-
El tablero de ajedrez es clave en este problema matemático.
-
Un tablero de ajedrez vacío, listo para el desafío.
-
Una representación visual del problema del trigo y el tablero.
-
Una ilustración que muestra cómo la segunda mitad del tablero acumula una cantidad mucho mayor.
Véase también
En inglés: Wheat and chessboard problem Facts for Kids
