Número taxicab para niños
Un número taxicab es un tipo especial de número que se puede escribir como la suma de dos números elevados al cubo de varias maneras diferentes. El nombre de estos números viene de una historia muy conocida entre los matemáticos G. H. Hardy y S. A. Ramanujan.
Contenido
¿Qué son los números Taxicab?
Un número taxicab, llamado Ta(n), es el número más pequeño que se puede expresar como la suma de dos números elevados al cubo (números positivos) de n maneras distintas. Un número elevado al cubo es, por ejemplo, 2x2x2 = 8 (que es 2 al cubo, o 2³).
El número 1729: Una historia curiosa
El número taxicab más famoso es el 1729, también conocido como Ta(2). Su historia es muy interesante. Un día, el matemático G. H. Hardy fue a visitar a su amigo, el brillante matemático S. A. Ramanujan, que estaba enfermo en el hospital. Hardy le comentó que había tomado un taxi con el número 1729 y que le parecía un número bastante aburrido.
Ramanujan, sin dudarlo, le respondió que el 1729 era un número muy especial. Le explicó que era el número más pequeño que se podía escribir como la suma de dos números elevados al cubo de dos maneras diferentes.
Aquí te mostramos cómo se puede hacer:
- 1729 = 1³ + 12³ (porque 1x1x1 = 1 y 12x12x12 = 1728, y 1 + 1728 = 1729)
- 1729 = 9³ + 10³ (porque 9x9x9 = 729 y 10x10x10 = 1000, y 729 + 1000 = 1729)
Esta anécdota muestra la increíble habilidad de Ramanujan con los números.
Ejemplos de números Taxicab
Aquí tienes algunos de los primeros números taxicab conocidos y cómo se forman:
- Ta(1) = 2
-
- Es el número más pequeño que se puede escribir como la suma de dos cubos de una sola manera:
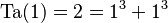
- Ta(2) = 1729
-
- Es el número más pequeño que se puede escribir como la suma de dos cubos de dos maneras diferentes:
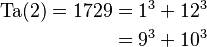
- Ta(3) = 87.539.319
-
- Este es el número más pequeño que se puede escribir como la suma de dos cubos de tres maneras distintas:
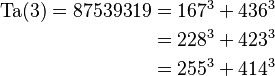
- Ta(4) = 6.963.472.309.248
-
- Es el número más pequeño que se puede escribir como la suma de dos cubos de cuatro maneras diferentes:
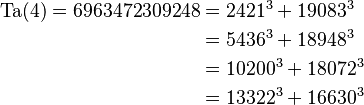
- Ta(5) = 48.988.659.276.962.496
-
- Este número se puede escribir como la suma de dos cubos de cinco maneras distintas:
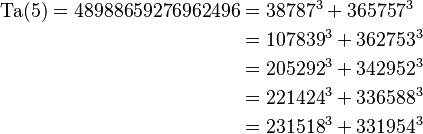
- Ta(6) = 24.153.319.581.254.312.065.344
-
- Este número se puede escribir como la suma de dos cubos de seis maneras diferentes:
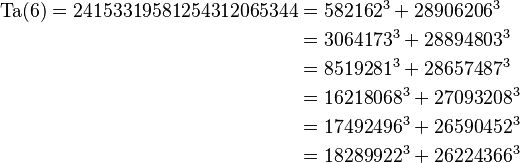
Límites superiores para números Taxicab
Para números taxicab más grandes, como Ta(7) o Ta(8), aún no se ha encontrado el número exacto más pequeño. Sin embargo, los matemáticos han descubierto "límites superiores". Esto significa que saben que el número taxicab real es igual o menor que el valor que han calculado. Estos límites superiores son números muy, muy grandes:
- Ta(7) es menor o igual a:
- Ta(8) es menor o igual a:
- Ta(9) es menor o igual a:
- Ta(10) es menor o igual a:
- Ta(11) es menor o igual a:
- Ta(12) es menor o igual a:
Véase también
 En inglés: Taxicab number Facts for Kids
En inglés: Taxicab number Facts for Kids
- Número cabtaxi
- Número de Hardy-Ramanujan
- Número Taxicab generalizado








