Método Schulze para niños

El método Schulze es una forma especial de contar votos que fue creada en 1997 por Markus Schulze. Este método ayuda a elegir a un ganador o a una lista de ganadores basándose en las preferencias de los votantes. Es útil cuando las personas no solo eligen a un candidato, sino que ordenan a todos los candidatos de su preferencia, del primero al último.

¿Cómo funciona el método Schulze?

El método Schulze es un poco complejo, pero su idea principal es encontrar al candidato que es el "más fuerte" en una competencia directa contra todos los demás. Imagina que cada candidato compite uno a uno con los demás.

Pasos principales del método

Para entender cómo se elige al ganador, el método Schulze sigue estos pasos:

• Paso 1: Contar los duelos. Primero, se compara a cada candidato con todos los demás. Por ejemplo, si hay un candidato A y un candidato B, se cuenta cuántos votantes prefieren A sobre B y cuántos prefieren B sobre A. Esto se hace para todas las posibles parejas de candidatos.
• Paso 2: Encontrar las rutas más fuertes. Después de contar los duelos, el método busca las "rutas más fuertes" entre los candidatos. Piensa en esto como un camino donde cada paso es una victoria de un candidato sobre otro. La fuerza de la ruta se mide por la victoria más débil en ese camino. El método busca el camino más fuerte posible de un candidato a otro.
• Paso 3: Determinar al ganador. Finalmente, el candidato que puede vencer a todos los demás candidatos (directa o indirectamente a través de una cadena de victorias fuertes) es el ganador. Si un candidato X tiene una ruta más fuerte para vencer a cualquier otro candidato Y, entonces X es mejor que Y. El ganador es el que es mejor que todos los demás.

Ejemplo sencillo del método Schulze

Imaginemos una votación con 45 personas y 5 candidatos: A, B, C, D y E. Los votantes ordenan a los candidatos según su preferencia. Por ejemplo, "5 ACBED" significa que 5 votantes prefirieron A primero, luego C, luego B, luego E y finalmente D.

• 5 votantes: A > C > B > E > D
• 5 votantes: A > D > E > C > B
• 8 votantes: B > E > D > A > C
• 3 votantes: C > A > B > E > D
• 7 votantes: C > A > E > B > D
• 2 votantes: C > B > A > D > E
• 7 votantes: D > C > E > B > A
• 8 votantes: E > B > A > D > C

Comparando candidatos uno a uno

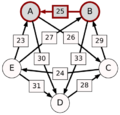
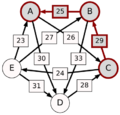
Vamos a comparar al candidato A con el candidato B:

• Votantes que prefieren A sobre B: 5 (ACBED) + 5 (ADECB) + 3 (CABED) + 7 (CAEBD) = 20 votantes.
• Votantes que prefieren B sobre A: 8 (BEDAC) + 2 (CBADE) + 7 (DCEBA) + 8 (EBADC) = 25 votantes.

En este caso, B le gana a A en una comparación directa (25 a 20).

Este tipo de comparación se hace para todas las parejas de candidatos.

Encontrando las rutas más fuertes

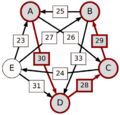
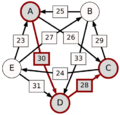
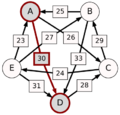
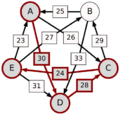
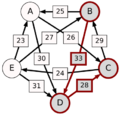
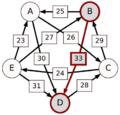
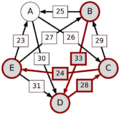
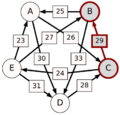
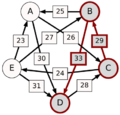
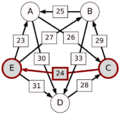
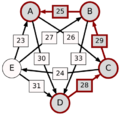
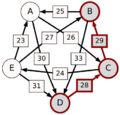
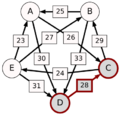
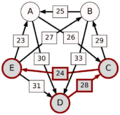
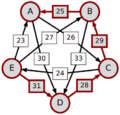
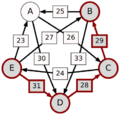
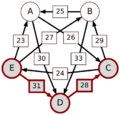
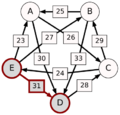
El método Schulze no solo mira las victorias directas, sino también las "rutas" de victorias. Por ejemplo, si A le gana a D con 30 votos, D le gana a C con 28 votos, y C le gana a E con 24 votos, entonces la ruta de A a E es A-(30)-D-(28)-C-(24)-E. La fuerza de esta ruta es el número más pequeño de votos en esa cadena, que en este caso es 24.

El método calcula la fuerza de la ruta más fuerte de cada candidato a cualquier otro.

En esta tabla, "p[X,Y]" significa la fuerza de la ruta más fuerte de X a Y.

• Si p[A,B] es 28 y p[B,A] es 25, significa que A es mejor que B (porque 28 es mayor que 25).
• Si p[E,D] es 31 y p[D,E] es 24, significa que E es mejor que D (porque 31 es mayor que 24).

¿Quién gana?

Siguiendo este proceso para todas las comparaciones, se puede determinar el orden final de los candidatos. En este ejemplo, el resultado es que E es el mejor, seguido por A, luego C, luego B y finalmente D. Por lo tanto, el candidato E es el ganador.

Galería de imágenes

• 

  Comparación de A y B

• 

  Comparación de A y C

• 

  Comparación de A y D

• 

  Comparación de A y E

• 

  Comparación de B y A

• 

  Comparación de B y C

• 

  Comparación de B y D

• 

  Comparación de B y E

• 

  Comparación de C y A

• 

  Comparación de C y B

• 

  Comparación de C y D

• 

  Comparación de C y E

• 

  Comparación de D y A

• 

  Comparación de D y B

• 

  Comparación de D y C

• 

  Comparación de D y E

• 

  Comparación de E y A

• 

  Comparación de E y B

• 

  Comparación de E y C

• 

  Comparación de E y D

Véase también

En inglés: Schulze method Facts for Kids