Muestreo (estadística) para niños

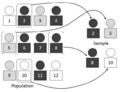
El muestreo es una técnica que nos ayuda a elegir una parte pequeña de un grupo grande para estudiarla. Imagina que tienes un montón de canicas de diferentes colores y quieres saber cuántas de cada color hay sin contarlas todas. El muestreo sería tomar un puñado de esas canicas para tener una idea.

Cuando elegimos una muestra de forma aleatoria, esperamos que lo que descubramos en esa parte pequeña sea parecido a lo que encontraríamos si estudiáramos todo el grupo. Esto nos permite ahorrar tiempo y dinero, y aun así obtener resultados muy útiles. Por ejemplo, en la investigación de nuevos medicamentos o en estudios de mercado, el muestreo es muy usado para entender a grupos grandes de personas.

Para que el muestreo funcione bien y los resultados sean confiables, debe seguir ciertas reglas. Aunque nunca podemos estar 100% seguros de que nuestra muestra sea perfecta, podemos hacer lo posible para que sea muy representativa.

Si el grupo que estudiamos (la población) es muy grande, podemos tomar varias muestras de él. Al conjunto de todas las muestras posibles que se pueden obtener de una población se le llama espacio muestral.

¿Qué es una población en el muestreo?

Para que un estudio de muestreo sea exitoso, es muy importante definir bien la "población". La población es el grupo completo de personas o cosas que tienen las características que queremos entender. Como casi nunca tenemos tiempo o dinero para estudiar a cada persona o elemento de una población, el objetivo es encontrar una muestra que sea una parte representativa de esa población.

A veces, es fácil saber cuál es la población. Por ejemplo, si una fábrica necesita saber si un lote de productos tiene buena calidad, el lote completo de productos es la población.

Otras veces, la población puede ser menos obvia. Por ejemplo, un investigador podría estudiar el tiempo que tardan las personas en la fila de un supermercado en diferentes momentos del día. Aquí, la población es el comportamiento de las filas a lo largo del tiempo. También, si se estudia el comportamiento de una máquina, la población sería todos los resultados posibles que esa máquina podría dar.

Incluso, a veces la población que estudiamos es una muestra de una "superpoblación" más grande. Por ejemplo, si se prueba un nuevo programa para dejar un hábito en un grupo pequeño de 100 personas, el objetivo es predecir cómo funcionaría ese programa si se aplicara a todas las personas del país. En este caso, la superpoblación es "todas las personas del país que podrían usar este tratamiento", un grupo que aún no existe por completo.

Es importante dedicar tiempo a definir bien la población que se va a muestrear y la población sobre la que queremos obtener información. Esto ayuda a aclarar muchas dudas y preguntas desde el principio.

Marco de muestreo: ¿Cómo encontramos la muestra?

En el muestreo, necesitamos una forma de identificar a cada elemento de la población para poder incluirlo en nuestra muestra. Esto se llama "marco de muestreo". El marco más sencillo es una lista de todos los elementos de la población, con su información de contacto. Por ejemplo, para una encuesta de opinión, un marco de muestreo podría ser una lista de votantes o una guía telefónica.

Una muestra probabilística es aquella en la que cada elemento de la población tiene una oportunidad conocida (mayor que cero) de ser elegido para la muestra. Esto nos permite hacer estimaciones precisas sobre la población.

Por ejemplo, si queremos saber el ingreso total de los adultos en una calle, podemos visitar cada casa, identificar a todos los adultos y elegir a uno al azar de cada casa. Si una persona vive sola, sus ingresos se cuentan tal cual. Si viven dos adultos, la persona elegida representa a ambos, y sus ingresos se contarían el doble para la estim estimación total. Esto asegura que todos tengan una probabilidad conocida de ser seleccionados.

Cuando cada elemento de la población tiene la misma probabilidad de ser elegido, se llama diseño de "igual probabilidad de selección" (EPS).

El muestreo probabilístico incluye varios métodos:

• Cada elemento tiene una probabilidad conocida y diferente de cero de ser elegido.
• Siempre hay un proceso de selección aleatoria en algún momento.

El muestreo aleatorio usa el azar para elegir la muestra. Si la probabilidad de que cada persona sea elegida se conoce de antemano, se llama muestreo probabilístico. A veces, se usa una muestra basada en la experiencia de alguien (muestreo por juicio) como una guía inicial antes de tomar una muestra aleatoria.

En los estudios, se pueden aplicar ajustes a los datos para que la muestra represente mejor a la población. La teoría de la probabilidad y la estadística nos ayudan a guiar estas prácticas.

Muestreo aleatorio simple

Este tipo de muestreo incluye todos los métodos donde se puede calcular la probabilidad de elegir cualquier muestra posible. Es el más recomendado, aunque no siempre se puede usar.

Tipos de muestreo aleatorio simple

• Sin reposición: Una vez que un elemento es elegido, no se puede volver a elegir. Por ejemplo, si pruebas la vida útil de una bombilla, no puedes probar la misma bombilla dos veces.
• Con reposición: Los elementos elegidos se pueden volver a elegir. En poblaciones muy grandes, la probabilidad de elegir el mismo elemento dos veces es tan pequeña que se considera como si fuera con reposición, aunque no lo sea.
• Con reposición múltiple: Similar al anterior, en poblaciones muy grandes, la probabilidad de repetir una elección es muy baja.

Para este tipo de muestreo, es muy útil usar números aleatorios generados por computadoras, calculadoras o tablas especiales.

Muestreo sistemático

Este método se usa cuando la población es muy grande o cuando el estudio se extiende en el tiempo. Primero, se identifican las unidades y se relacionan con un calendario si es necesario. Luego, se calcula un número llamado coeficiente de elevación (K):

K = N / n

Donde N es el tamaño de la población total y n es el tamaño de la muestra que queremos tomar.

Para empezar, se elige un número al azar entre 1 y K. A partir de ese número, se eligen los siguientes elementos a intervalos regulares de K. Por ejemplo, si K es 10, y el número al azar es 3, se elegirían los elementos 3, 13, 23, 33, y así sucesivamente.

Muestreo estratificado

Este método consiste en dividir la población en grupos o "estratos" que se parecen entre sí en alguna característica importante para el estudio. Por ejemplo, si estudias opiniones, podrías dividir la población en hombres y mujeres, porque sus opiniones podrían ser diferentes. A cada estrato se le asigna una "cuota", que es el número de personas de ese grupo que deben estar en la muestra. Dentro de cada estrato, a menudo se usa el muestreo sistemático.

Hay dos formas de asignar cuántos elementos se eligen de cada estrato:

• Asignación proporcional: El número de elementos de la muestra de cada estrato es proporcional al tamaño de ese estrato en la población. Si el 55% de la población son mujeres, el 55% de tu muestra también serán mujeres.
• Asignación óptima: Se eligen más individuos de los estratos que tienen más variedad en sus respuestas. Para esto, necesitas saber un poco sobre la población de antemano. Por ejemplo, si todos los hombres piensan igual, pero las mujeres tienen muchas opiniones diferentes, podrías tomar más mujeres en tu muestra para capturar esa variedad.

Muestreo por etapas múltiples

Esta técnica se usa cuando no hay una lista completa de toda la población o cuando una muestra simple o estratificada resultaría en unidades muy difíciles de alcanzar. En este método, la población se divide en varios niveles, y se van eligiendo muestras en cada nivel, como un embudo.

Por ejemplo, para estudiar a los maestros de primaria de un país, primero se podría elegir una muestra de distritos escolares (unidades primarias). Luego, de cada distrito escolar elegido, se selecciona una muestra de maestros (unidades secundarias).

Muestreo por conglomerados

Este método se usa cuando la población ya está dividida de forma natural en grupos llamados "conglomerados". Se supone que estos grupos son muy variados por dentro, es decir, representan bien a toda la población. Entonces, en lugar de elegir individuos de toda la población, se eligen solo algunos de estos grupos o conglomerados para el estudio.

Dentro de los grupos elegidos, se puede encuestar a todas las personas o solo a algunas, elegidas al azar. La ventaja de este método es que simplifica la recolección de información.

Si dentro de cada conglomerado elegido se seleccionan solo algunos individuos, se llama muestreo bietápico.

Las ideas de estratos y conglomerados son opuestas. Los estratos funcionan mejor si los grupos son muy parecidos por dentro (homogéneos) pero diferentes entre sí. Los conglomerados, en cambio, deben ser muy variados por dentro (heterogéneos) y muy parecidos entre sí.

Homogeneidad de las poblaciones o sus subgrupos

Cuando decimos "homogéneo" en muestreo, significa que no hay mucha variación. Los estratos funcionan mejor cuando cada uno de ellos es muy parecido en la característica que se mide. Por ejemplo, al estudiar la estatura, es útil separar a hombres y mujeres, porque dentro de cada grupo, las estaturas son más parecidas que si mezclamos a todos.

Si las diferencias dentro de un grupo son las mismas que en toda la población, entonces dividir en estratos no ayuda. En cambio, si hay grupos que ya contienen toda la variedad de la población, se usan conglomerados, lo que ahorra trabajo. En resumen, los estratos son mejores si los grupos son homogéneos, y los conglomerados son mejores si son heterogéneos y representan bien a la población.

El espacio muestral es el conjunto de todos los resultados posibles de un experimento aleatorio. Por ejemplo, al lanzar un dado, el espacio muestral es: 1, 2, 3, 4, 5, 6.

Muestreo no probabilístico

En este tipo de muestreo, no se puede calcular la probabilidad de que una muestra específica sea elegida, porque no todos tienen la misma oportunidad de ser seleccionados. Se usa para elegir a personas que saben mucho sobre el tema de estudio, ya que su información es muy valiosa.

Muestreo por cuotas

Es muy común en estudios de mercado y encuestas de opinión. Primero, se divide la población en estratos según características conocidas (como el género o la edad). Luego, se calcula qué porcentaje de la población representa cada estrato. Finalmente, se multiplica ese porcentaje por el tamaño total de la muestra para saber cuántas personas de cada estrato se necesitan. La diferencia con el muestreo estratificado es que, una vez que se sabe cuántas personas se necesitan de cada grupo, el investigador puede elegir libremente a quiénes encuestar dentro de ese grupo.

Muestreo de bola de nieve

Este método es útil para estudiar grupos difíciles de encontrar, minoritarios o muy dispersos, pero que tienen contacto entre sí. Consiste en identificar a algunas personas que cumplen los requisitos del estudio, y luego pedirles a ellas que nos ayuden a encontrar a otras personas con características similares. Es como una bola de nieve que crece al rodar.

Muestreo subjetivo por decisión razonada

Aquí, las personas de la muestra se eligen de forma intencional, basándose en algunas de sus características, no al azar. Una variación de esto es el muestreo compensado o equilibrado, donde se eligen las unidades de manera que el promedio de la muestra en ciertas características se acerque al promedio de la población. Esto se basa en referencias o recomendaciones.

Galería de imágenes

• 

  Representación visual del proceso de muestreo

Véase también

En inglés: Sample Facts for Kids

• error muestral
• muestra estadística
• tamaño de la muestra