Vector para niños
En matemática, un vector es como una flecha que tiene una dirección, un sentido y una longitud. Imagina que quieres describir cómo se mueve un coche: no solo necesitas saber qué tan rápido va (su velocidad), sino también hacia dónde se dirige. Para eso usamos los vectores.
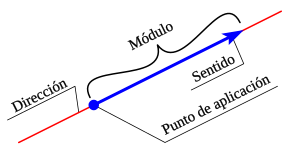
La longitud de esta "flecha" se llama módulo y siempre es un número positivo. La línea sobre la que se apoya el vector se llama recta soporte. La dirección del vector la dan todas las líneas paralelas a esta recta. El sentido es hacia dónde apunta la flecha en esa dirección.
En física, los vectores son muy útiles para describir cosas que necesitan más que un solo número. Por ejemplo, la velocidad, la fuerza o el desplazamiento (cambio de posición) son magnitudes vectoriales.
Plantilla:Ficha de concepto
Un vector se puede definir por su punto de inicio y su punto final. También se puede describir con números, llamados componentes, que nos dicen cuánto se mueve el vector en cada dirección (por ejemplo, hacia arriba, hacia un lado o hacia adelante).
Contenido
Conceptos clave de los vectores
Para entender bien los vectores, es importante conocer sus partes y cómo se usan.
¿Qué es un vector?
Un vector se puede ver de dos maneras:
- Como números: Un vector puede ser una lista de números. Por ejemplo, en un espacio de 3 dimensiones, un vector podría ser (2, 3, 1), que significa que se mueve 2 unidades en una dirección, 3 en otra y 1 en la tercera.
- Como una flecha: En geometría, un vector es una flecha que va de un punto inicial a un punto final.
Los elementos de un vector son:
- El punto de aplicación: Es el punto donde empieza la flecha.
- El módulo: Es la longitud de la flecha. Nos dice qué tan "grande" es el vector.
- La recta soporte: Es la línea imaginaria sobre la que se encuentra la flecha.
- La dirección: Es la orientación de la recta soporte.
- El sentido: Es hacia dónde apunta la flecha en esa dirección (por ejemplo, hacia arriba o hacia abajo).
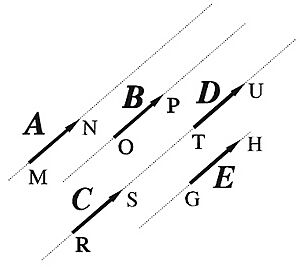
Cuando dos vectores tienen el mismo módulo, dirección y sentido, se consideran equivalentes. Esto significa que podemos mover un vector por el espacio sin cambiarlo, siempre que mantengamos su longitud, dirección y sentido.
Tipos de vectores
Los vectores se pueden clasificar de varias maneras:
- Vectores fijos o ligados: Tienen un punto de inicio específico.
- Vectores libres: Pueden empezar en cualquier punto del espacio.
- Vectores deslizantes: Su punto de inicio puede moverse a lo largo de su recta soporte.
- Vectores unitarios: Su módulo (longitud) es igual a 1.
- El vector nulo: Su módulo es 0, es decir, no tiene longitud ni dirección.
También podemos comparar vectores entre sí:
- Vectores paralelos: Tienen la misma dirección.
- Vectores opuestos: Tienen el mismo módulo y dirección, pero sentidos contrarios.
- Vectores perpendiculares: Sus direcciones forman un ángulo de 90 grados.
Cómo se escriben los vectores
Para escribir un vector, se usa una letra minúscula con una flecha encima (por ejemplo, 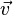 ) o en negrita (como v). Si es un vector fijo que va del punto P al punto Q, se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overrightarrow{PQ} .
) o en negrita (como v). Si es un vector fijo que va del punto P al punto Q, se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overrightarrow{PQ} .
El módulo de un vector se escribe poniendo el vector entre dos barras verticales, así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |\vec{v}| .
Componentes de un vector
Un vector en un espacio de tres dimensiones se puede expresar usando tres vectores unitarios especiales: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{i} , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{j} y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{k} . Estos vectores son perpendiculares entre sí y apuntan a lo largo de los ejes x, y, z.
Así, un vector 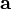 se puede escribir como:
se puede escribir como: 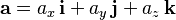 Donde
Donde 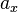 ,
, 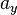 y
y 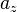 son las componentes del vector. También se pueden escribir como una lista de números: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{a} = (a_x,a_y,a_z) .
son las componentes del vector. También se pueden escribir como una lista de números: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{a} = (a_x,a_y,a_z) .
Operaciones con vectores
Podemos hacer varias operaciones con los vectores, siempre que estén en el mismo tipo de espacio.
Suma de vectores
Cuando sumamos dos vectores, el resultado es un tercer vector.
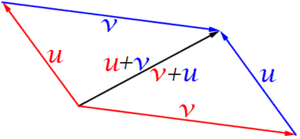
- Gráficamente: Para sumar dos vectores, puedes dibujar el primero y luego, desde el final del primero, dibujar el segundo. El vector suma es el que va desde el inicio del primer vector hasta el final del segundo. Es como seguir un camino: primero vas por un vector y luego por el otro, y el resultado es el camino directo desde el principio hasta el final.
- Con componentes: Si tienes los componentes de dos vectores, por ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v} = (v_1, v_2) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{w} = (w_1, w_2) , su suma es simplemente sumar los componentes correspondientes:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v} + \mathbf{w} = (v_1 + w_1, v_2 + w_2)
La suma de vectores tiene propiedades como la suma de números:
- El orden no importa: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v} + \mathbf{w} = \mathbf{w} + \mathbf{v} (propiedad conmutativa).
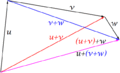
- Si sumas más de dos, el orden de las sumas parciales no importa: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w}) (propiedad asociativa).
- Existe un vector nulo (0,0) que, al sumarlo, no cambia el vector.
- Todo vector tiene un opuesto que, al sumarlo, da el vector nulo.
Multiplicación de un vector por un número (escalar)
Cuando multiplicas un vector por un número (llamado escalar), obtienes otro vector.
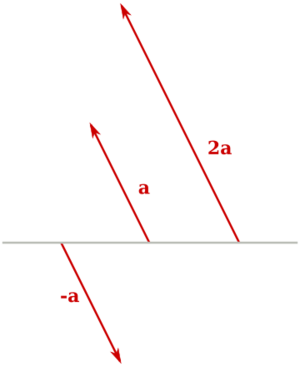
- Si el número es positivo, el nuevo vector tiene la misma dirección y sentido, pero su módulo se multiplica por ese número.
- Si el número es negativo, el nuevo vector tiene la misma dirección, pero el sentido opuesto, y su módulo se multiplica por el valor positivo del número.
- Con componentes: Si tienes un vector Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v} = (v_1, v_2) y un escalar
 , el producto es:
, el producto es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lambda \cdot \mathbf{v} = (\lambda \cdot v_1, \lambda \cdot v_2)
Combinaciones lineales
Una combinación lineal es cuando sumas varios vectores que han sido multiplicados por escalares. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1 \cdot \mathbf{v_1} + a_2 \cdot \mathbf{v_2} Donde 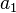 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_2 son números (escalares) y
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_2 son números (escalares) y 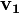 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v_2} son vectores.
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v_2} son vectores.
Producto escalar
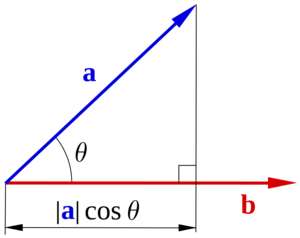
El producto escalar de dos vectores da como resultado un número (no un vector). Se calcula multiplicando los módulos de los vectores por el coseno del ángulo que hay entre ellos. Si los vectores son perpendiculares (forman un ángulo de 90 grados), su producto escalar es cero.
- Con componentes: Si tienes Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} = (u_1, u_2) y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v} = (v_1, v_2) , el producto escalar es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{u} \cdot \mathbf{v} = u_1 v_1 + u_2 v_2
Producto vectorial
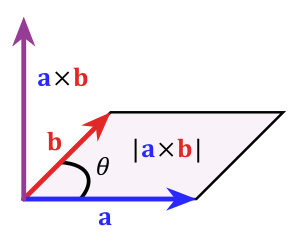
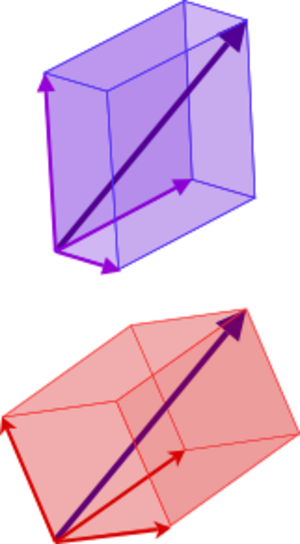
El producto vectorial de dos vectores (solo en 3 dimensiones) da como resultado otro vector. Este nuevo vector es perpendicular a los dos vectores originales. Su módulo es igual al producto de los módulos de los vectores por el seno del ángulo entre ellos. Su sentido se determina con la "regla de la mano derecha".
Si los vectores son paralelos, su producto vectorial es el vector nulo (cero).
Funciones con vectores
Podemos tener funciones que usan vectores. Por ejemplo, una función puede tomar un vector y devolver otro vector, o tomar un número y devolver un vector.
Transformaciones lineales
Las transformaciones lineales son funciones que toman un vector y lo "transforman" en otro vector, manteniendo ciertas propiedades. Por ejemplo, una transformación lineal puede rotar un vector, estirarlo o proyectarlo.
Se pueden representar con matrices. Si multiplicas la matriz de la transformación por el vector, obtienes el vector transformado.
Cambios de base
A veces, un vector se describe con componentes en un "sistema de coordenadas" (una base), y necesitamos saber cómo se vería en otro sistema de coordenadas. La función que hace esto se llama "cambio de base". Se usa una "matriz de cambio de base" para convertir las componentes de un sistema a otro.
Derivación de vectores
Si un vector cambia con el tiempo (por ejemplo, la posición de un objeto en movimiento), podemos calcular su derivada. La derivada de un vector nos dice cómo está cambiando ese vector. Por ejemplo, la derivada de la posición de un objeto es su velocidad.
- Con componentes: Si un vector Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}(t) = (v_1(t), v_2(t)) depende del tiempo
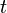 , su derivada se calcula derivando cada componente por separado:
, su derivada se calcula derivando cada componente por separado:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d}{dt}\mathbf{v}(t) = (\frac{dv_1}{dt}, \frac{dv_2}{dt})
Por ejemplo, si 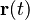 es el vector de posición de una partícula, su derivada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}(t) será el vector de velocidad de esa partícula.
es el vector de posición de una partícula, su derivada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{v}(t) será el vector de velocidad de esa partícula.
Ángulo entre dos vectores
El ángulo entre dos vectores 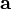 y
y 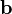 se puede encontrar usando el producto escalar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos \theta = \frac {\mathbf a \cdot \mathbf b}{|\mathbf{a}| \, |\mathbf{b}|}
se puede encontrar usando el producto escalar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos \theta = \frac {\mathbf a \cdot \mathbf b}{|\mathbf{a}| \, |\mathbf{b}|}
Vectores en física
Las magnitudes vectoriales son aquellas que, además de un número y una unidad, necesitan una dirección y un sentido para estar completamente definidas. Ejemplos son el desplazamiento, la velocidad, la aceleración y la fuerza.
Las magnitudes escalares, en cambio, solo necesitan un número y una unidad (como la masa, la temperatura o el volumen).
En física, es importante que los vectores representen algo real. Por ejemplo, en la mecánica de Newton, se usan vectores "polares" (como la fuerza) y "pseudovectores" o "vectores axiales" (como el momento angular o el campo magnético), que tienen propiedades especiales de transformación.
Galería de imágenes
-
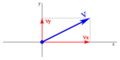
Componentes de un vector en Coordenadas cartesianas.
Véase también
 En inglés: Vector Facts for Kids
En inglés: Vector Facts for Kids


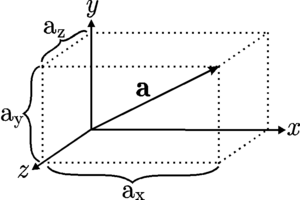
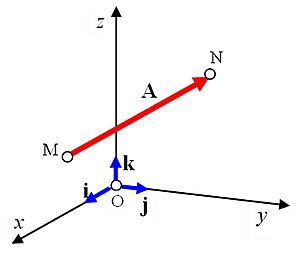
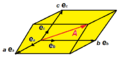
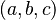 de un vector en 3 dimensiones.
de un vector en 3 dimensiones.