Intercambio de claves de Diffie-Hellman para niños

El protocolo Diffie-Hellman, creado por Whitfield Diffie y Martin Hellman en 1976, es una forma especial de que dos personas que nunca se han comunicado antes puedan ponerse de acuerdo sobre una clave secreta. Esto lo hacen a través de un canal de comunicación que no es seguro, es decir, donde alguien más podría estar escuchando.

Este método se usa principalmente para crear claves secretas que servirán para cifrar mensajes en una conversación. Aunque no verifica la identidad de las personas que se comunican, es la base para otros protocolos que sí lo hacen. Su seguridad se basa en que es muy, muy difícil calcular algo llamado "logaritmos discretos" en matemáticas.

Diffie y Hellman recibieron el Premio Turing en 2015 por este trabajo, que fue muy importante para la seguridad informática.

¿Cómo funciona el protocolo Diffie-Hellman?

Este sistema se basa en una idea ingeniosa: dos personas pueden crear una clave secreta juntas sin que un espía que esté escuchando sus mensajes pueda descubrirla.

Para lograrlo, eligen dos números que son públicos, es decir, que todos pueden conocer. Además, cada persona elige un número secreto que solo ella conoce. Usando una fórmula matemática que incluye potencias, cada uno realiza operaciones con los números públicos y su número secreto.

Luego, intercambian los resultados de estas operaciones de forma pública. Es muy difícil para un espía revertir estas operaciones y encontrar los números secretos originales. Por eso, se dice que el resultado es como una "función de un solo sentido".

Finalmente, cada persona usa una fórmula matemática que combina los resultados públicos del otro con su propio número secreto. Al hacer esto, ¡ambos llegan al mismo número! Ese número es la clave secreta compartida que usarán para proteger sus comunicaciones.

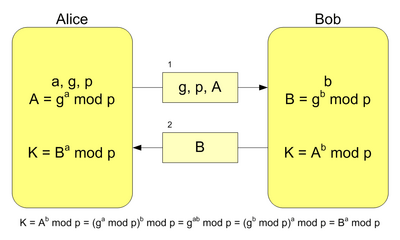
Pasos detallados del intercambio de claves

Diffie-Hellman.

Imaginemos que Alice y Bob quieren establecer una clave secreta, y hay un espía llamado Mallory que escucha todo. Así es como funciona:

• Primero, se eligen dos números públicos: un número primo grande llamado 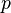y otro número llamado 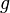. Estos números son conocidos por todos, incluyendo a Mallory.
• Alice elige un número secreto al azar, lo llamaremos . Luego, calcula un resultado usando la fórmula 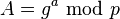y se lo envía a Bob.
• Bob también elige un número secreto al azar, lo llamaremos . Luego, calcula un resultado usando la fórmula 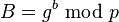y se lo envía a Alice.

Ahora, tanto Alice como Bob pueden calcular la misma clave secreta, que llamaremos .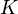

• Alice usa el número que recibió de Bob () y su propio número secreto () para calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): K = B^{a} \;\bmod\; p .
• Bob usa el número que recibió de Alice () y su propio número secreto () para calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): K = A^{b} \;\bmod\; p .

¡Ambos obtienen el mismo valor 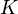! Esta es la clave secreta que compartirán.

¿Qué pasa si alguien intenta espiar?

Ataques pasivos (solo escuchar)

Si Mallory (el espía) conoce los números públicos (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p, g, A, B ), no puede calcular la clave secreta 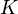a menos que conozca uno de los números secretos de Alice () o Bob (). Descubrir o a partir de o es un problema matemático muy difícil llamado "logaritmo discreto". Se cree que es casi imposible de resolver si los números primos son muy grandes.

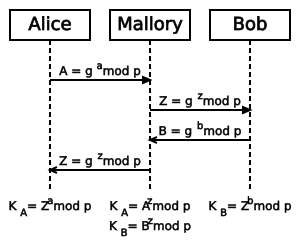
Ataques activos (intervenir la comunicación)

El protocolo Diffie-Hellman es vulnerable a un tipo de ataque llamado "Hombre en el medio" (Man-in-the-middle). Esto ocurre si un atacante se interpone en la comunicación entre Alice y Bob.

Ataque "Hombre en el medio" en Diffie-Hellman.

Así funciona el ataque:

• El atacante se hace pasar por Alice cuando habla con Bob, y se hace pasar por Bob cuando habla con Alice.
• El atacante establece una clave secreta con Alice y otra clave secreta diferente con Bob.
• Luego, el atacante retransmite los mensajes entre Alice y Bob, descifrándolos con una clave y volviéndolos a cifrar con la otra. De esta manera, puede leer y modificar toda la conversación sin que Alice o Bob se den cuenta.

Para evitar este tipo de ataque, se usan varias técnicas:

• Control de tiempos: Verificar que los mensajes lleguen en el momento esperado.
• Verificación de identidad: Asegurarse de que las personas que se comunican son quienes dicen ser. Esto se puede hacer con otros protocolos de seguridad.
• Verificación del contenido: Usar códigos especiales para asegurar que los mensajes no han sido alterados.
• Cifrado de claves públicas: Cifrar los números públicos con otro tipo de cifrado para evitar que sean interceptados.
• Uso de un tercero de confianza: Una tercera persona puede ayudar a verificar que la comunicación es segura.

Un ejemplo sencillo

Alice Secreto Cálculo p, g a ga mod p … (gb mod p)a mod p

=

Cálculo Secreto p, g b … gb mod p (ga mod p)b mod p

Alice y Bob deciden usar el número primo p=23 y la base g=5. Alice elige su número secreto a=6. Calcula 56 mod 23 = 8. Alice envía el 8 a Bob. Bob elige su número secreto b=15. Calcula 515 mod 23 = 19. Bob envía el 19 a Alice. Alice recibe el 19 de Bob. Calcula 196 mod 23 = 2. Bob recibe el 8 de Alice. Calcula 815 mod 23 = 2.

¡Ambos han llegado al número 2! Esta es su clave secreta compartida. En la vida real, se usan números mucho más grandes para que sea seguro.

Ejemplo con cifrado de mensajes

Imagina que Bob necesita enviarle un mensaje cifrado a Alice sin compartir la clave de cifrado directamente.

1. Alice elige su número secreto a=6, el número primo p=23 y la base g=5. Calcula 5⁶ mod 23 = 8. Alice le envía a Bob los números 8, 23 y 5.
2. Bob elige su número secreto b=15. Con los números que recibió de Alice (8, 23, 5) y su secreto (15), Bob calcula la clave de cifrado común: 8¹⁵ mod 23 = 2.
3. Bob usa esta clave (el número 2) para cifrar su mensaje con un método de cifrado simétrico (como AES).
4. Bob envía a Alice el mensaje cifrado y el número que él calculó con su secreto: 5¹⁵ mod 23 = 19.
5. Alice recibe el mensaje cifrado y el 19 de Bob. Con el 19 y su secreto (6), Alice calcula la clave de cifrado: 19⁶ mod 23 = 2.
6. Alice usa esa clave (el número 2) para descifrar el mensaje que le envió Bob.

Así, Bob pudo enviar un mensaje secreto a Alice sin que la clave de cifrado viajara por el canal de comunicación.

¿Se puede usar con más de dos personas?

Sí, la idea de Diffie-Hellman se puede extender para que más de dos personas puedan acordar una clave secreta. Por ejemplo, si Alice, Bob y Carol quieren una clave compartida, pueden seguir una serie de pasos donde cada uno va aplicando su número secreto a los resultados que recibe de los demás, hasta que todos llegan a la misma clave final.

Usos importantes del protocolo

El protocolo Diffie-Hellman se usa en muchos lugares para proteger nuestra información:

• La red Tor, que ayuda a navegar de forma más privada, usa Diffie-Hellman para crear claves secretas entre tu computadora y los diferentes puntos por los que pasa tu información. Esto ayuda a cifrar los datos en capas.
• El protocolo Off-the-Record Messaging (OTR), que se usa en algunas aplicaciones de mensajería instantánea, también se basa en Diffie-Hellman para cambiar la clave de cifrado constantemente mientras se intercambian mensajes.

Véase también

En inglés: Diffie–Hellman key exchange Facts for Kids