Homotecia para niños
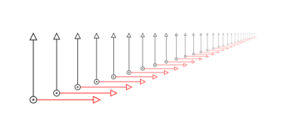
Una homotecia es una transformación geométrica que cambia el tamaño de una figura, haciéndola más grande o más pequeña, pero manteniendo su forma original. Imagina que tienes una foto y la amplías o la reduces; eso es similar a una homotecia.
Esta transformación se hace siempre desde un punto fijo, al que llamamos centro de la homotecia (O). También necesitamos un número, llamado razón (k), que nos dice cuánto se agranda o se encoge la figura.
Así, si tenemos un punto O y un número k (que no sea cero), una homotecia transforma cualquier punto P en un nuevo punto P'. Este nuevo punto P' estará en la misma línea que O y P. Además, la distancia de O a P' será k veces la distancia de O a P. Las figuras que se relacionan por una homotecia se llaman figuras homotéticas.
Contenido
¿Qué es una Homotecia?
Una homotecia es como una "fotocopiadora" de figuras. Toma una figura y crea una copia que es más grande o más pequeña, pero siempre con la misma forma y orientación.
Para entenderlo mejor, piensa en un punto central (C) y un número (k). Si tienes un punto M, la homotecia lo mueve a un nuevo punto M' de tal manera que:
- El punto M' está en la misma línea que C y M.
- La distancia de C a M' es k veces la distancia de C a M.
Si k es un número positivo, la figura se mantiene del mismo lado del centro. Si k es negativo, la figura se "voltea" y aparece al otro lado del centro.
Propiedades Clave de las Homotecias
Las homotecias tienen características muy interesantes:
- Mantienen la línea: Si varios puntos están en una línea recta, sus imágenes (los puntos transformados) también estarán en una línea recta.
- Conservan el centro: Si un punto es el centro de un segmento (la mitad de una línea), su imagen también será el centro del segmento transformado.
- Líneas paralelas: Una línea y su imagen siempre serán paralelas entre sí.
- Ángulos iguales: Los ángulos de la figura original son iguales a los ángulos de la figura transformada. Esto significa que la forma de la figura no cambia, solo su tamaño.
- Punto fijo: Si la razón k no es 1, el único punto que no se mueve es el centro de la homotecia. Si k es 1, la figura no cambia en absoluto.
- Simetría: Si la razón k es -1, la homotecia es como un espejo que voltea la figura alrededor del centro.
¿Cómo afecta la razón (k) a la figura?
El valor de la razón k nos dice mucho sobre la transformación:
- Si el valor absoluto de k (es decir, k sin considerar si es positivo o negativo) es mayor que 1 (por ejemplo, 2 o -3), la figura se amplía (se hace más grande).
- Si el valor absoluto de k es menor que 1 (por ejemplo, 0.5 o -0.8), la figura se reduce (se hace más pequeña).
- Si k es negativo, la figura no solo cambia de tamaño, sino que también se invierte o se voltea con respecto al centro.
Homotecias en el Plano
En un plano (como una hoja de papel), una homotecia es una transformación donde cualquier línea y su imagen son paralelas. Esto significa que las homotecias no cambian los ángulos, por eso se les llama "transformaciones conformes".
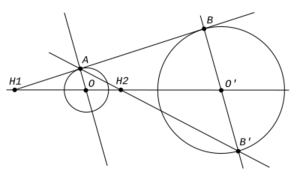
Imagina dos círculos de diferente tamaño. Siempre podemos encontrar una homotecia que transforme uno en el otro.
- Si los círculos están del mismo lado del centro de homotecia, la razón k será positiva.
- Si los círculos están en lados opuestos del centro de homotecia, la razón k será negativa.
Ejes de Homotecia
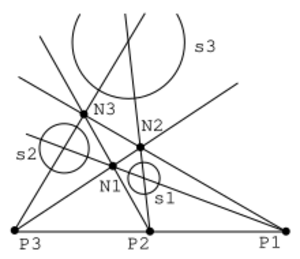
Cuando tenemos dos círculos, siempre podemos pensar que uno es la imagen del otro mediante una homotecia. Esto significa que hay un punto (o dos) que actúa como centro de esa homotecia.
Si tenemos tres círculos, la cosa se pone más interesante. Podemos encontrar varios centros de homotecia entre ellos. Lo curioso es que estos centros de homotecia a menudo se alinean en grupos de tres, formando lo que llamamos ejes de homotecia. Estas líneas son importantes en la geometría.
Ver también
Véase también
 En inglés: Dilation (geometry) Facts for Kids
En inglés: Dilation (geometry) Facts for Kids