Factor de conversión para niños
El factor de conversión o factor unidad es una herramienta muy útil en matemáticas y ciencias. Imagina que quieres cambiar una medida de una unidad a otra, por ejemplo, de centímetros a metros. Este método te permite hacerlo multiplicando por una o varias fracciones especiales. En estas fracciones, la parte de arriba (numerador) y la parte de abajo (denominador) representan la misma cantidad, pero están escritas con unidades diferentes. Esto hace que cada una de estas fracciones sea igual a uno, ¡como si multiplicaras por 1! Es una forma muy efectiva de cambiar unidades y resolver problemas sencillos sin usar la regla de tres.
¿Cómo funciona el Factor de Conversión?
Para usar un factor de conversión, necesitas conocer una equivalencia, que es una igualdad entre dos cantidades. Por ejemplo, sabemos que 1 pulgada es igual a 2.54 centímetros. Con esta información, podemos crear una fracción que nos ayude a convertir.
Construyendo un Factor de Conversión
Un factor de conversión se crea a partir de una equivalencia. Por ejemplo, si sabemos que 1 kilómetro es igual a 1000 metros, podemos escribir dos factores de conversión:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1 \text{ km}}{1000 \text{ m}}
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1000 \text{ m}}{1 \text{ km}}
Ambas fracciones son iguales a 1, porque el numerador y el denominador representan la misma cantidad. Elegimos la que nos ayude a "cancelar" la unidad que no queremos y obtener la que sí queremos.
Ejemplos Prácticos de Conversión
Veamos algunos ejemplos para entenderlo mejor.
Convertir Pulgadas a Centímetros
Si queremos pasar 15 pulgadas a centímetros, y sabemos que 1 pulgada es igual a 2.54 centímetros:
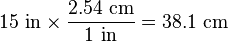
Aquí, el factor de conversión Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\textstyle \frac{2.54 \text{ cm}}{1 \text{ in}} } nos permite "eliminar" las pulgadas y quedarnos con los centímetros.
Convertir Velocidad: Metros por Segundo a Kilómetros por Hora
Imagina que un coche va a 25 metros por segundo y quieres saber cuántos kilómetros por hora son. Necesitamos dos equivalencias:
- 1 kilómetro es igual a 1000 metros
- 1 hora es igual a 3600 segundos
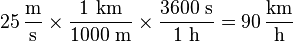
En este caso, usamos dos factores de conversión. El primero cambia los metros a kilómetros y el segundo cambia los segundos a horas. Las unidades que no queremos se "cancelan" (una está arriba y la otra abajo), dejando solo las unidades que buscamos.
Ejemplos con Simplificación de Unidades
Es muy útil ver cómo las unidades se "cancelan" en el proceso.
Pasar 2 días y medio a horas
Sabemos que 1 día tiene 24 horas.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2,5\cancel{\mbox{días}}\times\frac{24\mbox{ h}}{1\cancel{\mbox{dia}}}= \frac{2,5\ \cancel{\mbox{días}}\times 24\mbox{ h}}{1\ \cancel{\mbox{dia}}}= 60\mbox{ h}
Aquí, la unidad "días" se cancela, y el resultado queda en "horas".
Pasar 30 cm/s a km/h
Para convertir 30 centímetros por segundo a kilómetros por hora, necesitamos varias equivalencias:
- 1 metro = 100 centímetros
- 1 kilómetro = 1000 metros
- 1 minuto = 60 segundos
- 1 hora = 60 minutos
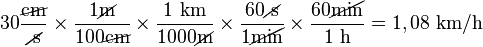
Como puedes ver, las unidades "centímetros", "metros", "segundos" y "minutos" se cancelan, y solo quedan "kilómetros" y "horas", que son las unidades que buscábamos.
Véase también
 En inglés: Conversion of units Facts for Kids
En inglés: Conversion of units Facts for Kids
- Número adimensional
- Sistemas de unidades

