Exponenciación modular para niños

La exponenciación modular es una operación matemática especial que se usa mucho en las computadoras, sobre todo para mantener la información segura. Imagina que es como un truco de magia con números que ayuda a proteger tus mensajes y datos en internet.

Esta operación calcula el residuo (lo que sobra) cuando un número, llamado base (b), se eleva a una cierta potencia o exponente (e), y luego el resultado se divide por otro número, llamado módulo (m). En matemáticas, se escribe así: 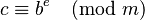. Aquí, c es el resultado final.

Por ejemplo, si tenemos b = 5, e = 3 y m = 13, la exponenciación modular nos pide calcular el resto de dividir 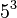(que es 125) entre 13. El resultado es 8, porque 125 dividido por 13 es 9 con un resto de 8. Así, c = 8.

Si los números b, e y m son positivos y b es menor que m, siempre habrá una única solución c que será mayor o igual a 0 y menor que m.

A veces, el exponente e puede ser un número negativo. En esos casos, se usa un truco matemático llamado "inverso multiplicativo modular" para encontrar la solución.

Los problemas de exponenciación modular son fáciles de resolver para las computadoras, incluso con números muy grandes. Sin embargo, el problema contrario, que es encontrar el exponente e cuando ya conoces b, c y m, es muy difícil. Esta diferencia hace que la exponenciación modular sea perfecta para usarla en la criptografía, que es el arte de codificar y descodificar mensajes para protegerlos.

Exponenciación Modular: ¿Qué es y para qué sirve?

La exponenciación modular es una operación matemática que combina la exponenciación (elevar un número a una potencia) con la aritmética modular (trabajar con los restos de las divisiones). Es una herramienta fundamental en el mundo digital.

Entendiendo la Exponenciación Modular

Para entenderla mejor, piensa en un reloj. Si son las 10 y sumas 5 horas, no son las 15, sino las 3. Esto es aritmética modular con un módulo de 12. La exponenciación modular hace algo similar, pero con potencias.

¿Cómo se calcula? Un ejemplo sencillo

Imagina que quieres calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^{13} \pmod{497} . Esto significa: ¿cuál es el resto de dividir 4 elevado a la potencia 13 entre 497?

El número b es la base (4), e es el exponente (13) y m es el módulo (497).

¿Por qué es importante en la informática?

Esta operación es clave en la ciencias de la computación porque permite realizar cálculos complejos de forma eficiente. Es especialmente útil en áreas donde la seguridad de la información es vital.

La magia de la criptografía

La exponenciación modular es el corazón de muchos algoritmos criptográficos. Estos algoritmos son como códigos secretos que protegen tu información. Por ejemplo, cuando inicias sesión en una página web o envías un mensaje, la exponenciación modular ayuda a que tus datos viajen de forma segura y nadie más pueda leerlos. Su característica de ser "fácil de calcular en una dirección, pero muy difícil en la contraria" la hace ideal para crear sistemas de seguridad robustos.

Métodos para calcular la Exponenciación Modular

Existen diferentes maneras de calcular la exponenciación modular. Algunas son más sencillas pero lentas, y otras son más complejas pero mucho más rápidas, especialmente con números muy grandes.

Método Directo: Paso a Paso

El método más sencillo es calcular primero la potencia completa y luego encontrar el resto. Por ejemplo, para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^{13} \pmod{497} :

• Primero, calculamos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^{13} , que es 67.108.864.
• Luego, dividimos 67.108.864 entre 497. El resto de esta división es 445.

Así, el resultado es 445.

Este método funciona bien con números pequeños. Pero en criptografía, la base b y el exponente e pueden ser números gigantes, con cientos de dígitos. Calcular una potencia tan grande primero y luego dividirla sería muy lento y requeriría muchísima memoria en la computadora.

Método con Menos Memoria: Más Eficiente

Para evitar trabajar con números tan grandes, existe un método que va calculando el resto en cada paso de la multiplicación. Esto reduce la cantidad de memoria necesaria.

El algoritmo funciona así:

1. Empezamos con un resultado temporal (c) igual a 1 y un contador (e) igual a 0.
2. Aumentamos el contador e' en 1.
3. Calculamos el nuevo resultado temporal: c = (base × c) % módulo.
4. Si e es menor que el exponente original e, volvemos al paso 2. Si no, c es la respuesta final.

Veamos el ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^{13} \pmod{497} con este método:

• e = 1. c = (4 × 1) % 497 = 4.
• e = 2. c = (4 × 4) % 497 = 16.
• e = 3. c = (4 × 16) % 497 = 64.
• e = 4. c = (4 × 64) % 497 = 256.
• e = 5. c = (4 × 256) % 497 = 1024 % 497 = 30.
• e = 6. c = (4 × 30) % 497 = 120.
• e = 7. c = (4 × 120) % 497 = 480.
• e = 8. c = (4 × 480) % 497 = 1920 % 497 = 429.
• e = 9. c = (4 × 429) % 497 = 1716 % 497 = 225.
• e = 10. c = (4 × 225) % 497 = 900 % 497 = 403.
• e = 11. c = (4 × 403) % 497 = 1612 % 497 = 121.
• e = 12. c = (4 × 121) % 497 = 484.
• e = 13. c = (4 × 484) % 497 = 1936 % 497 = 445.

El resultado final es 445, igual que con el método directo. Este método es mejor porque los números intermedios nunca se hacen tan grandes.

El Método Más Rápido: Exponenciación Binaria

El método más eficiente y usado en la práctica se llama exponenciación binaria o "por cuadrados". Este método es mucho más rápido, especialmente con exponentes muy grandes.

La clave es convertir el exponente e a su forma binaria (usando solo 0s y 1s). Por ejemplo, el número 13 en binario es 1101.

El algoritmo aprovecha que cualquier potencia se puede descomponer en potencias de 2. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^{13} = b^{8} \cdot b^{4} \cdot b^{1} .

Un ejemplo de cómo funciona este método en un lenguaje de programación (como C#) sería: Bignum modpow(Bignum base, Bignum exp, Bignum m) {

Bignum result = 1;

while (exp > 0) { if ((exp & 1) > 0) result = (result * base) % m; exp >>= 1; base = (base * base) % m; }

return result;

}

Vamos a usar el ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^{13} \pmod{497} con este método. El exponente 13 en binario es 1101.

• Paso 1: base = 4, exp = 1101 (binario), result = 1.
  • El último dígito de exp es 1. Entonces, result = (1 × 4) % 497 = 4.
  • exp se convierte en 110 (quitando el último dígito).
  • base se convierte en (4 × 4) % 497 = 16.
• Paso 2: base = 16, exp = 110 (binario), result = 4.
  • El último dígito de exp es 0. result no cambia.
  • exp se convierte en 11.
  • base se convierte en (16 × 16) % 497 = 256.
• Paso 3: base = 256, exp = 11 (binario), result = 4.
  • El último dígito de exp es 1. Entonces, result = (4 × 256) % 497 = 1024 % 497 = 30.
  • exp se convierte en 1.
  • base se convierte en (256 × 256) % 497 = 65536 % 497 = 429.
• Paso 4: base = 429, exp = 1 (binario), result = 30.
  • El último dígito de exp es 1. Entonces, result = (30 × 429) % 497 = 12870 % 497 = 445.
  • exp se convierte en 0.
  • base se convierte en (429 × 429) % 497 = 184041 % 497 = 151. (Esta última operación ya no es necesaria porque exp es 0).

El bucle termina porque exp es 0. El resultado final es 445, el mismo que con los otros métodos. Este método es el más rápido porque el número de pasos depende de la cantidad de dígitos binarios del exponente, no del valor del exponente en sí.

Véase también

En inglés: Modular exponentiation Facts for Kids