Convexidad para niños
La convexidad es una característica de las formas que se parecen a la parte exterior de una pelota o una burbuja. Imagina que tienes una pelota: su superficie es convexa porque sobresale hacia afuera. Es lo contrario de la concavidad, que se parece a la parte interior de un cuenco.
En matemáticas, un grupo de puntos o una forma se considera convexa si, al tomar dos puntos cualesquiera dentro de esa forma, la línea recta que los une siempre se mantiene completamente dentro de la forma. Es como si pudieras ir de un punto a otro en línea recta sin salirte de los límites de esa figura.
Contenido
¿Qué significa que un conjunto sea convexo?
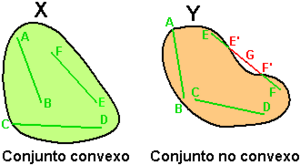
Un conjunto de puntos (o una figura) es convexo si para cualquier par de puntos que elijas dentro de él, el segmento de línea que los conecta también está completamente dentro del conjunto.
Por ejemplo, un círculo es un conjunto convexo. Si tomas dos puntos dentro de un círculo y los unes con una línea recta, esa línea siempre estará dentro del círculo. Lo mismo ocurre con un cuadrado o un triángulo.
Sin embargo, una forma de "C" no es convexa. Si tomas un punto en un extremo de la "C" y otro en el otro extremo, la línea recta que los une saldrá de la forma.
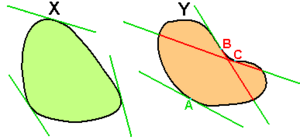
Si una forma tiene bordes suaves (sin esquinas), podemos pensar en las líneas que la tocan en un solo punto (llamadas tangentes). Una forma es convexa si siempre se encuentra del mismo lado de cada una de sus líneas tangentes. Esto significa que las líneas tangentes nunca "atraviesan" la forma. Esta idea también funciona para formas con esquinas, como los polígonos convexos.
¿Qué es la envoltura convexa de un conjunto?
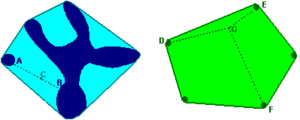
La envoltura convexa de un conjunto de puntos es el conjunto convexo más pequeño que contiene a todos esos puntos. Imagina que tienes varios puntos dispersos en una hoja de papel. Si pones una goma elástica alrededor de todos ellos y la dejas encogerse, la forma que crea la goma elástica es la envoltura convexa de esos puntos.
Por ejemplo, si tienes cinco puntos, su envoltura convexa podría ser un polígono que los encierra a todos. Si tienes una forma irregular, su envoltura convexa sería la forma convexa que la "envuelve" por completo, rellenando cualquier "hueco" o "curva hacia adentro".
¿Qué es una función convexa?
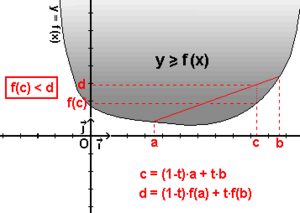
Una función convexa es un tipo especial de función matemática. Imagina que dibujas la gráfica de una función en un plano. Si la región del plano que está por encima de la curva de la función es un conjunto convexo, entonces la función es convexa.
Una manera más sencilla de entenderlo es que si tomas dos puntos cualquiera en la curva de una función convexa y trazas una línea recta entre ellos, esa línea siempre estará por encima o tocando la curva de la función. Nunca estará por debajo.
Algunos ejemplos de funciones convexas son:
- La función y = x2 (una parábola que se abre hacia arriba).
- La función exponencial y = ex.
Si una función es convexa, su gráfica se "curva hacia arriba" o es una línea recta.
¿Cuál es la diferencia entre convexidad y concavidad?
La convexidad y la concavidad son conceptos opuestos. Si una forma o una función es convexa, su "inverso" o su "reflejo" es cóncavo.
Por ejemplo, si una función f es cóncava, significa que la función -f (su opuesto) es convexa. Piensa en una parábola que se abre hacia arriba (convexa) y una que se abre hacia abajo (cóncava).
Las únicas funciones que son tanto convexas como cóncavas al mismo tiempo son las funciones lineales (las que se representan con una línea recta).
Generalizaciones de la convexidad
La idea de convexidad se puede extender a otros tipos de formas y espacios, más allá de las figuras simples que vemos en un plano.
Conjuntos en forma de estrella
Un conjunto es en forma de estrella (o estrella-convexo) si hay al menos un punto dentro del conjunto desde el cual puedes trazar una línea recta a cualquier otro punto del conjunto sin salirte.
Un conjunto convexo siempre es en forma de estrella. Sin embargo, un conjunto en forma de estrella no siempre es convexo. Imagina una estrella de cinco puntas: es en forma de estrella (puedes ir desde el centro a cualquier punta sin salirte), pero no es convexa (si unes dos puntas opuestas, la línea sale de la estrella).
Convexidad ortogonal
Un conjunto es ortogonalmente convexo si cualquier segmento de línea que sea paralelo a los ejes de coordenadas (horizontal o vertical) y que conecte dos puntos del conjunto, se encuentra totalmente dentro del conjunto. Esto es útil en áreas como el diseño de circuitos.
Convexidad en otras geometrías
La convexidad también se puede aplicar en geometrías que no son la euclidiana (la que usamos normalmente). En estas geometrías, en lugar de líneas rectas, se usan las "geodésicas", que son los caminos más cortos entre dos puntos. Un conjunto es geodésicamente convexo si contiene las geodésicas que unen dos puntos cualesquiera dentro de él.
Véase también
 En inglés: Convex set Facts for Kids
En inglés: Convex set Facts for Kids
- Concavidad
- Conjunto conexo
- Función convexa
- Curva convexa
- Envolvente convexa
- Dominio en estrella