Coeficiente de Poisson para niños
El coeficiente de Poisson es un número especial que nos ayuda a entender cómo se comportan los materiales cuando los estiramos o los apretamos. Imagina que tienes una banda elástica y la estiras: se hace más larga, ¿verdad? Pero también notarás que se vuelve más delgada. El coeficiente de Poisson mide precisamente eso: cuánto se adelgaza (o ensancha) un material en sus lados cuando lo estiramos (o comprimimos) a lo largo.
Este coeficiente lleva el nombre de un científico francés llamado Simeon Poisson. La mayoría de los materiales que usamos, como el metal o el plástico, tienen un coeficiente de Poisson que va de 0.0 a 0.5. Por ejemplo, el caucho, que es muy blando y elástico, tiene un coeficiente cercano a 0.5. Esto significa que cuando lo estiras, se adelgaza mucho. En cambio, materiales como el corcho tienen un coeficiente cercano a cero, lo que significa que casi no cambian de ancho cuando los aprietas.
Contenido
¿Qué es el Efecto Poisson?
El coeficiente de Poisson mide algo llamado el efecto Poisson. Este efecto es la tendencia de un material a ensancharse en las direcciones que son perpendiculares a la fuerza que lo está apretando. Por el contrario, si estiras un material, este tiende a encogerse en las direcciones transversales (los lados).
Piensa en una goma elástica: cuando la estiras, se hace más fina. El coeficiente de Poisson nos dice la relación entre cuánto se encoge de lado y cuánto se estira a lo largo.
En algunos casos muy raros, un material puede hacer lo contrario: encogerse de lado cuando lo aprietas, o ensancharse de lado cuando lo estiras. A estos materiales se les llama materiales auxéticos, y tienen un coeficiente de Poisson negativo. ¡Es como si se hicieran más gordos al estirarlos!
Para que un material sea estable, su coeficiente de Poisson debe estar entre -1.0 y +0.5. La mayoría de los aceros y plásticos rígidos tienen un valor de alrededor de 0.3. El caucho tiene un valor cercano a 0.5. El corcho, como mencionamos, está cerca de 0.
¿Cómo se calcula el Coeficiente de Poisson?
El coeficiente de Poisson se calcula dividiendo cuánto cambia el ancho de un material entre cuánto cambia su largo, cuando se le aplica una fuerza.
Se usa la siguiente fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \nu = -\frac{\text{cambio de ancho relativo}}{\text{cambio de largo relativo}}
Donde:
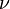 es el coeficiente de Poisson.
es el coeficiente de Poisson.- El "cambio de ancho relativo" es cuánto se encoge o ensancha el material en sus lados, dividido por su ancho original.
- El "cambio de largo relativo" es cuánto se estira o acorta el material a lo largo, dividido por su largo original.
El signo negativo se usa porque, generalmente, si el largo aumenta (se estira), el ancho disminuye (se encoge), y viceversa.
Cambio en el ancho
Si tienes una varilla con un diámetro (o ancho) original 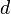 y una longitud
y una longitud 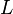 , y la estiras de modo que su longitud cambia en
, y la estiras de modo que su longitud cambia en 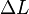 , entonces su diámetro
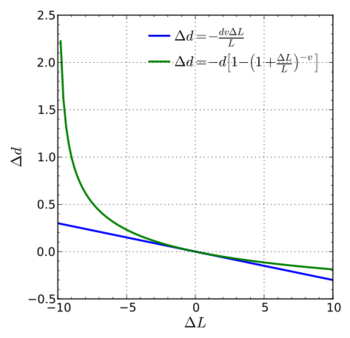
, entonces su diámetro 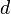 cambiará en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta d .
cambiará en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \Delta d .
Para cambios pequeños, la relación es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\Delta d}{d} = -\nu \frac{\Delta L}{L}
Esto significa que el cambio en el diámetro es proporcional al cambio en la longitud y al coeficiente de Poisson. El valor es negativo porque el diámetro disminuye cuando la longitud aumenta.
Cambio en el volumen
El coeficiente de Poisson también nos ayuda a entender cómo cambia el volumen total de un material cuando se estira o se comprime.
Para cambios pequeños, el cambio relativo de volumen Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\Delta V}{V} se puede aproximar con la fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\Delta V}{V} \approx (1-2\nu)\frac{\Delta L}{L}
Si el coeficiente de Poisson es 0.5 (como en el caucho), entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1-2 \times 0.5) = 0 , lo que significa que el volumen casi no cambia cuando el material se deforma. Esto es lo que ocurre con los materiales que son casi "incompresibles".
Materiales Comunes y sus Coeficientes
El coeficiente de Poisson no tiene unidades. Aquí te mostramos algunos valores típicos:
- Caucho: Cerca de 0.5. Se adelgaza mucho al estirarse.
- Acero: Alrededor de 0.27 a 0.30.
- Aluminio: Alrededor de 0.33.
- Corcho: Cerca de 0.0. Casi no cambia de ancho al comprimirse.
- Vidrio: Entre 0.18 y 0.30.
Materiales Auxéticos (Coeficiente de Poisson Negativo)
Como mencionamos, algunos materiales especiales llamados auxéticos tienen un coeficiente de Poisson negativo. Esto significa que cuando los estiras, ¡se hacen más anchos en lugar de más delgados! Esto es muy inusual y se debe a la forma en que están organizados sus átomos o estructuras internas. Estos materiales son muy interesantes para nuevas tecnologías.
Véase también
 En inglés: Poisson's ratio Facts for Kids
En inglés: Poisson's ratio Facts for Kids



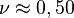 .
.