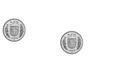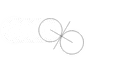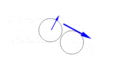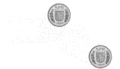Choque elástico para niños

En física, un choque elástico (o colisión elástica) ocurre cuando dos o más objetos chocan y, después del impacto, la energía de movimiento total del sistema se mantiene igual. Esto significa que no se pierde energía en forma de sonido, calor o deformaciones permanentes en los objetos.

Imagina que tienes dos canicas que chocan. Si el choque es elástico, la energía que tenían las canicas antes de chocar es la misma que tienen después. Además, la "cantidad de movimiento" (que es una combinación de la masa y la velocidad de un objeto) también se mantiene igual en todo el sistema. Esto sucede porque las fuerzas que actúan durante el choque son internas a los objetos que chocan.

Cuando un choque es elástico, los objetos rebotan sin cambiar su forma de manera permanente. No se escucha un gran ruido ni se genera calor significativo. Si, por el contrario, un choque produce deformaciones, sonido o calor, se le llama choque inelástico, porque parte de la energía de movimiento se transforma en otras formas de energía. También existen los choques explosivos, donde la energía de movimiento aumenta después del impacto, como cuando un resorte se dispara al contacto.

¿Cómo funcionan los choques elásticos en una línea?

Entendiendo las colisiones frontales

Para entender mejor los choques elásticos, podemos imaginar dos objetos que se mueven en la misma línea y chocan de frente. Piensa en dos carritos de juguete que se deslizan uno hacia el otro. Los científicos usan fórmulas para predecir qué tan rápido se moverá cada objeto después de la colisión, basándose en sus masas y velocidades iniciales. Lo importante es que, en un choque elástico, tanto la cantidad de movimiento como la energía de movimiento total se conservan.

Ejemplos de choques elásticos: ¿Qué sucede en diferentes situaciones?

Colisiones con masas iguales

Imagina que dos bolas de billar idénticas chocan de frente. Si una de ellas se mueve y la otra está quieta, después del choque, la primera bola se detendrá y la segunda saldrá disparada con la misma velocidad que tenía la primera. Es como si la energía de movimiento se transfiriera completamente de una a la otra.

Dos masas iguales chocan elásticamente. Se observa la transferencia total de momento lineal de una masa a la otra, de tal modo que después del impacto, la que tenía movimiento ahora se queda estática mientras que la que estaba en reposo adquiere una velocidad igual a la que se desplazaba la primera, de tal modo que el momento lineal y la energía cinética se conserve.

Colisiones de un objeto pequeño contra uno mucho más grande

Piensa en una pelota de tenis que golpea una pared muy grande y sólida. La pared es tan masiva que apenas se mueve. La pelota rebota con casi la misma velocidad con la que llegó, pero en dirección opuesta. La pared actúa como un obstáculo fijo, y la pelota simplemente "rebota" sin que la pared cambie su movimiento de forma notable.

Colisiones de un objeto grande contra uno mucho más pequeño

Ahora, imagina un camión chocando con una pequeña pelota de ping-pong (si la pelota fuera elástica y no se aplastara). El camión casi no cambiaría su velocidad, como si nada hubiera pasado. Sin embargo, la pequeña pelota saldría disparada con una velocidad mucho mayor, ¡casi el doble de la velocidad del camión! Esto se debe a que el objeto grande tiene mucha más cantidad de movimiento y energía.

Choque elástico entre dos cuerpos de distinta masa moviéndose con igual rapidez en sentidos opuestos.

Choque elástico entre dos monedas. En esta animación se muestra como se modifican los momentos de lineales de cada moneda individual (representado por una flecha azul), de tal modo que el momento lineal total del sistema sea el mismo antes y después de la colisión (flecha roja).

Mientras la radiación de cuerpo negro no escape de un sistema, los átomos en agitación térmica experimentan esencialmente colisiones elásticas. En promedio, los átomos rebotan entre sí manteniendo la misma energía cinética después de cada colisión. Aquí, los átomos de helio a temperatura ambiente se muestran retrasados dos trillones de veces. Cinco átomos están coloreados de rojo para facilitar el seguimiento de sus movimientos.

Galería de imágenes

• 

  Dos masas iguales chocan elásticamente. Se observa la transferencia total de momento lineal de una masa a la otra, de tal modo que después del impacto, la que tenía movimiento ahora se queda estática mientras que la que estaba en reposo adquiere una velocidad igual a la que se desplazaba la primera, de tal modo que el momento lineal y la energía cinética se conserve.

• 

  Choque elástico entre dos cuerpos de distinta masa moviéndose con igual rapidez en sentidos opuestos.

• 

  Choque elástico entre dos monedas. En esta animación se muestra como se modifican los momentos de lineales de cada moneda individual (representado por una flecha azul), de tal modo que el momento lineal total del sistema sea el mismo antes y después de la colisión (flecha roja).

• 

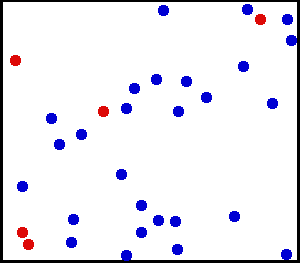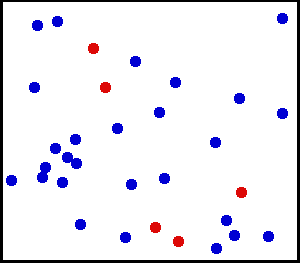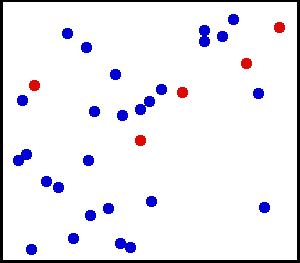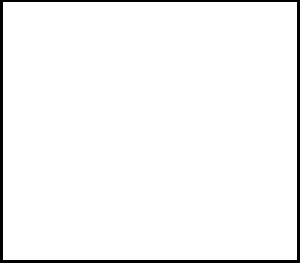
  Mientras la radiación de cuerpo negro no escape de un sistema, los átomos en agitación térmica experimentan esencialmente colisiones elásticas. En promedio, los átomos rebotan entre sí manteniendo la misma energía cinética después de cada colisión. Aquí, los átomos de helio a temperatura ambiente se muestran retrasados dos trillones de veces. Cinco átomos están coloreados de rojo para facilitar el seguimiento de sus movimientos.

Véase también

En inglés: Elastic collision Facts for Kids

• Energía cinética
• Conservación de la energía
• Choque inelástico
• Choque (física)