Archivo: Twisted square antiprism

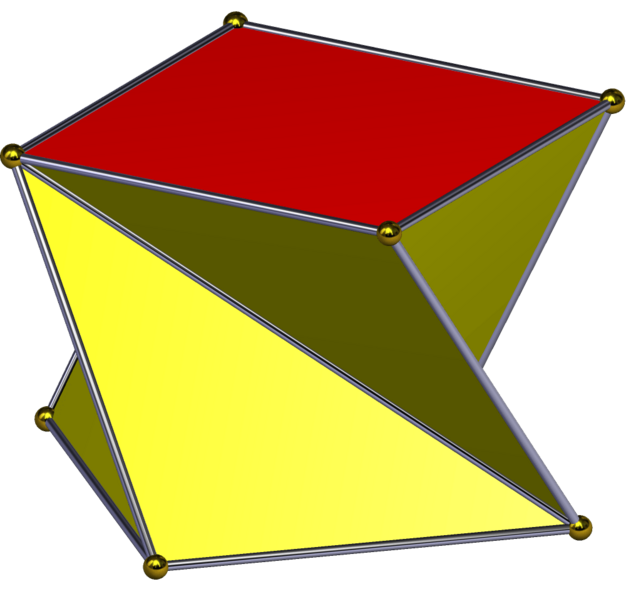
Descripción: This solid can be called a twisted square prism because it can be formed by "twisting" a square prism. But there are two ways one can "twist" a square prism (or rectangular prism): If I physically twist a clay prism, the four connecting squares (or rectangles) become twisted parallelograms (not the solid shown). If I rotate the top square relative to the bottom square, and only allow straight edges and planar faces, nothing "slips" or "snaps" (like with the gyrobicupolae). I must replace the four connecting squares (or rectangles) with four pairs of triangles (as shown here). That operation seems like more than just "twisting". Also, the resulting "twisted prism is topologically identical to the antiprism" – a prism becomes an antiprism for any twist other than 0 degrees. If I rotate the top square relative to the bottom square of a uniform [or regular] square antiprism, the triangles change proportions, but the number of faces does not change. "Twisted square antiprism" names this solid unambiguously, and is in use for it (Twisted antiprism on Wolfram), so it seems preferable.
Título: Twisted square antiprism
Créditos: Trabajo propio
Autor(a): Tomruen
Términos de Uso: Creative Commons Attribution-Share Alike 4.0
Licencia: CC BY-SA 4.0
Enlace de Licencia: https://creativecommons.org/licenses/by-sa/4.0
¿Se exige la atribución?: Sí